48. 手写字符识别神经网络#
48.1. 介绍#
上一个实验中,我们从感知机出发对人工神经网络的原理进行了介绍,并结合理论推导详细阐述了神经网络反向传播的过程。本次挑战中,我们将结合 scikit-learn 提供的人工神经网络实现方法,完成手写字符识别。
48.2. 知识点#
人工神经网络
手写字符识别
48.3. 手写字符数据集概览#
本次挑战中,我们将使用手写字符数据集 DIGITS。该数据集的全称为 Pen-Based Recognition of Handwritten Digits Data Set,来源于 UCI 开放数据集网站。
数据集包含由 1797 张数字 0 到 9
的手写字符影像转换后的数字矩阵,目标值是
0-9。为了方便,这里直接使用 scikit-learn 提供的
load_digits
方法加载该数据集。
import numpy as np
from sklearn import datasets
digits = datasets.load_digits()
加载完成的 DIGITS 数据集中包含 3 个属性:
属性 |
描述 |
|---|---|
|
|
8x8 矩阵,记录每张手写字符图像对应的像素灰度值 |
|
|
将 images 对应的 8x8 矩阵转换为行向量 |
|
|
记录 1797 张影像各自代表的数字 |
下面,我们输出第一个手写字符查看。
第一个字符图像对应的数字:
digits.target[0]
0
第一个字符图像对应的灰度值矩阵:
digits.images[0]
array([[ 0., 0., 5., 13., 9., 1., 0., 0.],
[ 0., 0., 13., 15., 10., 15., 5., 0.],
[ 0., 3., 15., 2., 0., 11., 8., 0.],
[ 0., 4., 12., 0., 0., 8., 8., 0.],
[ 0., 5., 8., 0., 0., 9., 8., 0.],
[ 0., 4., 11., 0., 1., 12., 7., 0.],
[ 0., 2., 14., 5., 10., 12., 0., 0.],
[ 0., 0., 6., 13., 10., 0., 0., 0.]])
将矩阵扁平化为行向量:
digits.data[0]
array([ 0., 0., 5., 13., 9., 1., 0., 0., 0., 0., 13., 15., 10.,
15., 5., 0., 0., 3., 15., 2., 0., 11., 8., 0., 0., 4.,
12., 0., 0., 8., 8., 0., 0., 5., 8., 0., 0., 9., 8.,
0., 0., 4., 11., 0., 1., 12., 7., 0., 0., 2., 14., 5.,
10., 12., 0., 0., 0., 0., 6., 13., 10., 0., 0., 0.])
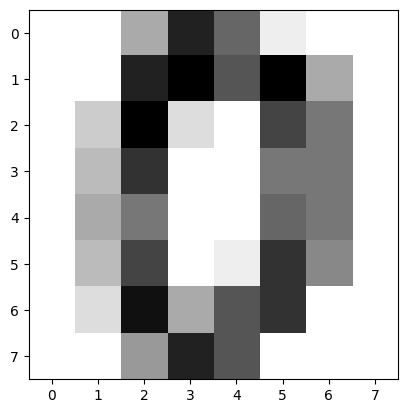
你可能感觉到数字总是不太直观。那么,我们可以根据灰度值矩阵,使用 Matplotlib 把字符对应的灰度图像绘制出来。
from matplotlib import pyplot as plt
%matplotlib inline
image1 = digits.images[0]
plt.imshow(image1, cmap=plt.cm.gray_r)
上面的图像可以很明显看出来是手写字符 0。
Exercise 48.1
挑战:使用 \(1 \times 5\) 的子图样式绘制 Digits 数据集前 5 个手写字符的图像。
## 代码开始 ### (3~5 行代码)
## 代码结束 ###
参考答案 Exercise 48.1
### 代码开始 ### (3~5 行代码)
fig, axes = plt.subplots(1, 5, figsize=(12,4))
for i, image in enumerate(digits.images[:5]):
axes[i].imshow(image, cmap=plt.cm.gray_r)
### 代码结束 ###
期望输出
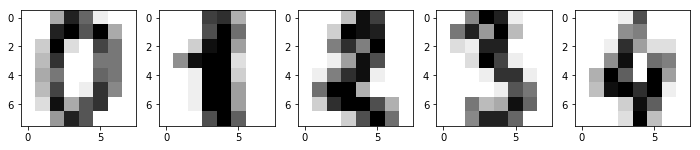
接下来,我们需要将数据集随机切分为训练集和测试集,以备后用。
Exercise 48.2
挑战:使用
train_test_split()
将数据集切分为 80%(训练集) 和 20%(测试集) 两部分。
规定:训练集特征,训练集目标,测试集特征,测试集目标分别定义为:X_train,
y_train,
X_test,
y_test,随机数种子定为 30。
## 代码开始 ### (≈ 2 行代码)
## 代码结束 ###
参考答案 Exercise 48.2
### 代码开始 ### (≈ 2 行代码)
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(digits.data, digits.target, test_size=0.2, random_state=30)
### 代码结束 ###
运行测试
len(X_train), len(y_train), len(X_test), len(y_test), np.mean(y_test[5:13])
期望输出
(1437, 1437, 360, 360, 3.75)
48.4. 使用 scikit-learn 搭建人工神经网络#
scikit-learn 中的
MLPClassifier()
类实现了具有反向传播算法的多层神经网络结构。
sklearn.neural_network.MLPClassifier(hidden_layer_sizes=(100, ), activation='relu', solver='adam', alpha=0.0001, batch_size='auto', learning_rate='constant', learning_rate_init=0.001, power_t=0.5, max_iter=200, shuffle=True, random_state=None, tol=0.0001, verbose=False, warm_start=False, momentum=0.9, nesterovs_momentum=True, early_stopping=False, validation_fraction=0.1, beta_1=0.9, beta_2=0.999, epsilon=1e-08)
该类的参数较多,我们介绍主要参数如下:
- hidden_layer_sizes: 定义隐含层及包含的神经元数量,(20, 20) 代表 2 个隐含层各有 20 个神经元。 - activation: 激活函数,有 identity(线性), logistic, tanh, relu 可选。 - solver: 求解方法,有 lbfgs(拟牛顿法),sgd(随机梯度下降),adam(改进型 sgd) 可选。adam 在相对较大的数据集上效果比较好(上千个样本),对小数据集而言,lbfgs 收敛更快效果也很好。 - alpha: 正则化项参数。 - learning_rate: 学习率调整策略,constant(不变),invscaling(逐步减小),adaptive(自适应) 可选。 - learning_rate_init: 初始学习率,用于随机梯度下降时更新权重。 - max_iter: 最大迭代次数。 - shuffle: 决定每次迭代是否重新打乱样本。 - random_state: 随机数种子。 - tol: 优化求解的容忍度,当两次迭代损失差值小于该容忍度时,模型认为达到收敛并且训练停止。
接下来,我们准备使用
MLPClassifier()
构建一个神经网络预测模型。
Exercise 48.3
挑战:使用
MLPClassifier()
搭建神经网络结构,并训练手写字符识别模型,最后得到在测试集上的预测准确率。
规定:
-
神经网络结构包含
2个隐含层,依次有100和50个神经元。 -
使用
relu作为激活函数。 -
使用随机梯度下降
SGD方法求解。 -
学习率为
0.02且在学习过程中保持不变。 -
最大迭代次数为
100次。 -
随机数种子设为
1。 其余参数使用默认值。
from sklearn.neural_network import MLPClassifier
from sklearn.metrics import accuracy_score
def mpl():
"""
参数:无
返回:
model -- 人工神经网络模型
score -- 测试集上的预测准确率
"""
### 代码开始 ### (≈ 2 行代码)
model = None
score = None
### 代码结束 ###
return model, score
参考答案 Exercise 48.3
from sklearn.neural_network import MLPClassifier
from sklearn.metrics import accuracy_score
def mpl():
"""
参数:无
返回:
model -- 人工神经网络模型
score -- 测试集上的预测准确率
"""
### 代码开始 ### (≈ 2 行代码)
model = MLPClassifier(
hidden_layer_sizes=(100, 50),
activation='relu',
solver='sgd',
learning_rate_init=0.02,
learning_rate='constant',
max_iter=100,
random_state=1
)
model.fit(X_train, y_train)
score = accuracy_score(y_test, model.predict(X_test))
### 代码结束 ###
return model, score
运行测试
mpl()[1]
期望输出
> 0.95
按照上面参数训练出来的神经网络一般准确率可以达到
\(98\%\)
左右。我们可以输出
model
的一些属性,例如迭代的次数以及绘制迭代损失变化曲线。
# 绘制损失变化曲线
model = mpl()[0]
plt.plot(model.loss_curve_)
# 输出模型达到收敛的迭代次数
model.n_iter_
○ 欢迎分享本文链接到你的社交账号、博客、论坛等。更多的外链会增加搜索引擎对本站收录的权重,从而让更多人看到这些内容。