15. 高斯分布函数实现及绘图#
15.1. 介绍#
朴素贝叶斯实验中提到了高斯分布,本次挑战通过 Python 实现高斯分布函数,并使用 Matplotlib 绘制不同参数下的高斯分布图像。
15.2. 知识点#
高斯分布公式
高斯分布函数
15.3. 高斯分布公式#
在朴素贝叶斯的实验中,我们知道可以依照特征数据类型,在计算先验概率时对朴素贝叶斯模型进行划分,并分为:多项式模型,伯努利模型和高斯模型。而在前面的实验中,我们使用了多项式模型来完成。
很多时候,当我们的特征是连续变量时,运用多项式模型的效果不好。所以,我们通常会采用高斯模型对连续变量进行处理,而高斯模型实际上就是假设连续变量的特征数据是服从高斯分布。其中,高斯分布函数表达式为:
其中 \(\mu\) 为均值,\(\sigma\) 为标准差。
Exercise 15.1
挑战:参考高斯分布公式,使用 Python 实现高斯分布函数。
"""实现高斯分布函数
"""
import numpy as np
def Gaussian(x, u, d):
"""
参数:
x -- 变量
u -- 均值
d -- 标准差
返回:
p -- 高斯分布值
"""
### 代码开始 ### (≈ 3~5 行代码)
p = None
return p
### 代码结束 ###
参考答案 Exercise 15.1
"""实现高斯分布函数
"""
import numpy as np
def Gaussian(x, u, d):
"""
参数:
x -- 变量
u -- 均值
d -- 标准差
返回:
p -- 高斯分布值
"""
### 代码开始 ### (≈ 3~5 行代码)
d_2 = d * d * 2
zhishu = -(np.square(x - u) / d_2)
exp = np.exp(zhishu)
pi = np.pi
xishu = 1 / (np.sqrt(2 * pi) * d)
p = xishu * exp
return p
### 代码结束 ###
运行测试
x = np.linspace(-5, 5, 100)
u = 3.2
d = 5.5
g = Gaussian(x, u, d)
len(g), g[10]
期望输出
(100,
0.030864654760573856)
实现高斯分布函数之后,我们可以使用 Matplotlib 绘制出不同参数下的高斯分布图像。
Exercise 15.2
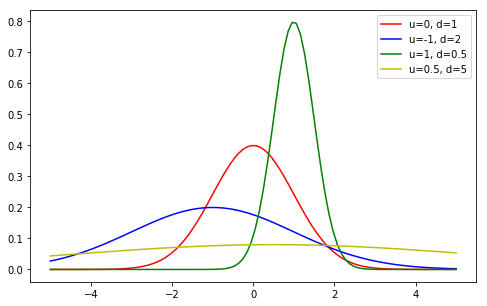
挑战:按规定的参数绘制高斯分布图像。
规定:
-
绘制 4 组高斯分布线形图像,\(\mu\) 和 \(\sigma\) 分别为:
(0, 1), (-1, 2), (1, 0.5), (0.5, 5)。 -
4 组高斯分布图像的线形颜色分别为红色、蓝色、绿色、黄色。
-
绘制图例,并以 \(u=\sigma\) 样式呈现。
from matplotlib import pyplot as plt
%matplotlib inline
## 代码开始 ### (≈ 5~10 行代码)
## 代码结束 ###
参考答案 Exercise 15.2
from matplotlib import pyplot as plt
%matplotlib inline
### 代码开始 ### (≈ 5~10 行代码)
y_1 = Gaussian(x, 0, 1)
y_2 = Gaussian(x, -1, 2)
y_3 = Gaussian(x, 1, 0.5)
y_4 = Gaussian(x, 0.5, 5)
plt.figure(figsize=(8,5))
plt.plot(x, y_1, c='r', label="u=0, d=1")
plt.plot(x, y_2, c='b', label="u=-1, d=2")
plt.plot(x, y_3, c='g', label="u=1, d=0.5")
plt.plot(x, y_4, c='y', label="u=0.5, d=5")
plt.legend()
### 代码结束 ###
期望输出
○ 欢迎分享本文链接到你的社交账号、博客、论坛等。更多的外链会增加搜索引擎对本站收录的权重,从而让更多人看到这些内容。
