57. PyTorch 实现线性回归#
57.1. 介绍#
前面的实验已经对 PyTorch 的使用进行了详细介绍，相信你已经对 PyTorch 的张量类型，常用的运算方法，以及构建神经网络的流程比较熟悉了。本次挑战中，需要你使用 PyTorch 实现再熟悉不过的线性回归。线性回归固然简单，但挑战的目的在于熟悉对 PyTorch 的使用。
57.2. 知识点#
PyTorch 原理及使用
nn.Module 类实现线性回归
线性回归已经是我们的老朋友了，课程一开始就已经对其进行了深入的介绍。如果用一句话来概括线性回归，那就是在输入和输出数据之间通过线性方法进行建模。
首先，我们生成本次挑战所需要的示例数据。这里，我们使用 PyTorch 提供的 API 来操作。
import torch
from matplotlib import pyplot as plt
%matplotlib inline
torch.manual_seed(10) # 随机数种子
x = torch.linspace(1, 10, 50) # 生成等间距张量
y = 2 * x + 3 * torch.rand(50)
plt.style.use("ggplot") # 使用 ggplot 绘图样式
plt.scatter(x, y)
<matplotlib.collections.PathCollection at 0x12ea2de40>
57.3. 实现线性回归模型#
前面的实验内容说过
torch.nn.Module
类是所有神经网络的基类，它既可以表示神经网络中的某层，也可以表示若干层的神经网络。接下来，你将通过继承
torch.nn.Modules
类来实现挑战所需的
LinearRegressionModel()
线性回归类。
Exercise 57.1
挑战：继承
torch.nn.Module
类实现挑战所需的
LinearRegressionModel()
线性回归类。
规定：只能使用 PyTorch 提供的类和方法。
提示：可能会用到
nn.Linear()
线性变换层。
import torch.nn as nn
## 代码开始 ### (> 5 行代码)
## 代码结束 ###
参考答案 Exercise 57.1
import torch.nn as nn
### 代码开始 ### (> 5 行代码)
class LinearRegressionModel(nn.Module):
def __init__(self):
super(LinearRegressionModel, self).__init__()
self.linear = nn.Linear(1, 1)
def forward(self, x):
out = self.linear(x)
return out
### 代码结束 ###
运行测试
LinearRegressionModel()
期望输出
LinearRegressionModel(
(linear): Linear(in_features=1, out_features=1, bias=True)
)
本次挑战不会使用最小二乘法来求解线性回归参数，而是使用迭代法。所以，首先需要定义损失函数以及优化器。挑战将会选择 MSE 的值作为损失函数，并通过 SGD 算法求解。
Exercise 57.2
挑战：定义 MSE 损失函数及随机梯度下降优化器。
规定：随机梯度下降优化器的学习率设为 0.01，其余使用默认参数。
提示：可能会用到实验中提到的损失函数和优化器。
model = LinearRegressionModel() # 实例化模型
## 代码开始 ### (≈ 2 行代码)
loss_fn = None
opt = None
## 代码开始 ### (≈ 3 行代码)
参考答案 Exercise 57.2
model = LinearRegressionModel() # 实例化模型
### 代码开始 ### (≈ 2 行代码)
loss_fn = nn.MSELoss() # 定义损失函数
opt = torch.optim.SGD(model.parameters(), lr=0.01) # 定义优化器
### 代码开始 ### (≈ 3 行代码)
运行测试
loss_fn, opt
期望输出
(MSELoss(), SGD (
Parameter Group 0
dampening: 0
lr: 0.01
momentum: 0
nesterov: False
weight_decay: 0
))
一切准备就绪，接下来就是训练模型并求解线性回归参数。
Exercise 57.3
挑战：完成线性回归参数优化迭代过程。
规定：迭代次数为 100 次。
提示：注意输入数据的形状问题。思路是先前向传递得到真实值，计算损失并通过优化器迭代。
## 代码开始 ### (> 5 行代码)
## 代码结束 ###
参考答案 Exercise 57.3
### 代码开始 ### (> 5 行代码)
iters = 100
for i in range(iters):
x = x.reshape(len(x), 1) # 输入 x 张量
y = y.reshape(len(x), 1) # 输入 y 张量
y_ = model(x) # 前向传播
loss = loss_fn(y_, y) # 计算损失
opt.zero_grad() # 优化器梯度清零，否则会累计
loss.backward() # 从最后 loss 开始反向传播
opt.step() # 优化器迭代
if (i+1) % 10 == 0:
print('Iteration [{}/{}], Loss: {:.3f}'
.format(i+1, iters, loss.item()))
### 代码结束 ###
期望输出：（loss 数值不同没有关系）
Iteration [ 10/100], Loss: 0.791
Iteration [ 20/100], Loss: 0.784
Iteration [ 30/100], Loss: 0.778
Iteration [ 40/100], Loss: 0.772
Iteration [ 50/100], Loss: 0.767
Iteration [ 60/100], Loss: 0.762
Iteration [ 70/100], Loss: 0.757
Iteration [ 80/100], Loss: 0.753
Iteration [ 90/100], Loss: 0.749
Iteration [100/100], Loss: 0.745
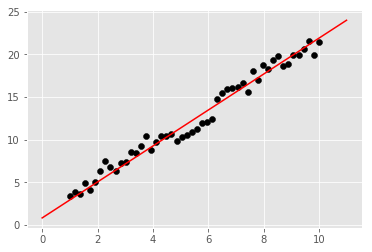
最后，同样需要将拟合后直线绘制到原散点图中查看效果。
Exercise 57.4
挑战：根据拟合参数，将拟合直线绘制到图像中。
提示：通过
model.state_dict()
读取拟合参数。
## 代码开始 ### (≈ 4 行代码)
## 代码结束 ###
参考答案 Exercise 57.4
### 代码开始 ### (≈ 4 行代码)
weight = model.state_dict()['linear.weight'] # 权重
bias = model.state_dict()['linear.bias'] # 偏置项
plt.scatter(x, y, c='black')
plt.plot([0, 11], [bias, weight * 11 + bias], 'r')
### 代码结束 ###
期望输出
○ 欢迎分享本文链接到你的社交账号、博客、论坛等。更多的外链会增加搜索引擎对本站收录的权重，从而让更多人看到这些内容。