9. 回归方法综合应用练习#
9.1. 介绍#
本次挑战将会结合前面学习到的相关回归分析方法,完成一个多元回归分析任务。同时,我们将结合 NumPy,scikit-learn,SciPy,statsmodels 等库,复习不同方法的实现及应用。
9.2. 知识点#
一元线性回归
多元线性回归
假设检验
挑战使用《An Introduction to Statistical
Learning》书中提供的
Advertising
示例数据集用于练习。该书是统计学习经典著作,有兴趣的话可以从作者网站
免费下载阅读。
首先,我们加载并预览该数据集。
# 下载数据集
!wget -nc https://cdn.aibydoing.com/aibydoing/files/advertising.csv
import pandas as pd
data = pd.read_csv("advertising.csv", index_col=0,)
data.head()
| tv | radio | newspaper | sales | |
|---|---|---|---|---|
| 1 | 230.1 | 37.8 | 69.2 | 22.1 |
| 2 | 44.5 | 39.3 | 45.1 | 10.4 |
| 3 | 17.2 | 45.9 | 69.3 | 9.3 |
| 4 | 151.5 | 41.3 | 58.5 | 18.5 |
| 5 | 180.8 | 10.8 | 58.4 | 12.9 |
数据集包含 4 列,共 200 行。每个样本代表某超市销售相应单位件商品所需要支出的广告费用。以第一行为例,表示该超市平均销售 22.1 件商品,需要支出的电视广告费用,广播广告费用以及报刊广告费用为:230.1 美元,37.8 美元和 69.2 美元。
所以,本次挑战将前 3 列视作特征,最后一列视作目标值。
Exercise 9.1
挑战:使用 SciPy 提供的普通最小二乘法分别计算 3 个特征与目标之间的一元线性回归模型拟合参数。
规定:需使用
scipy.optimize.leastsq
函数完成计算,并直接输出函数结果无需处理。
import numpy as np
from scipy.optimize import leastsq
## 代码开始 ### (≈ 10 行代码)
params_tv = None
params_radio = None
params_newspaper = None
## 代码结束 ###
params_tv[0], params_radio[0], params_newspaper[0]
参考答案 Exercise 9.1
import numpy as np
from scipy.optimize import leastsq
### 代码开始 ### (≈ 10 行代码)
p_init = np.random.randn(2)
def func(p, x):
w0, w1 = p
f = w0 + w1*x
return f
def err_func(p, x, y):
ret = func(p, x) - y
return ret
params_tv = leastsq(err_func, p_init, args=(data.tv, data.sales))
params_radio = leastsq(err_func, p_init, args=(data.radio, data.sales))
params_newspaper = leastsq(err_func, p_init, args=(data.newspaper, data.sales))
### 代码结束 ###
params_tv[0], params_radio[0], params_newspaper[0]
期望输出
((array([7.03259354, 0.04753664]), (array([9.31163807, 0.20249578]), (array([12.35140711, 0.0546931]))
接下来,我们根据最小二乘法求得的结果,将拟合直线绘制到原分布散点图中。
Exercise 9.2
挑战:以横向子图的方式绘制 3 个特征分别与目标之间的散点图,并添加线性拟合直线。
规定:线性拟合直线开始于散点图中最小横坐标值,结束于最大横坐标值,并以红色显示。
from matplotlib import pyplot as plt
%matplotlib inline
## 代码开始 ### (≈ 10 行代码)
## 代码结束 ###
参考答案 Exercise 9.2
from matplotlib import pyplot as plt
%matplotlib inline
### 代码开始 ### (≈ 10 行代码)
fig, axes = plt.subplots(1, 3, figsize=(16, 4))
data.plot(kind='scatter', x='tv', y='sales', ax=axes[0])
data.plot(kind='scatter', x='radio', y='sales', ax=axes[1])
data.plot(kind='scatter', x='newspaper', y='sales', ax=axes[2])
x_tv = np.array([data.tv.min(), data.tv.max()])
axes[0].plot(x_tv, params_tv[0][1]*x_tv + params_tv[0][0], 'r')
x_radio = np.array([data.radio.min(), data.radio.max()])
axes[1].plot(x_radio, params_radio[0][1]*x_radio + params_radio[0][0], 'r')
x_newspaper = np.array([data.newspaper.min(), data.newspaper.max()])
axes[2].plot(x_newspaper, params_newspaper[0][1] *
x_newspaper + params_newspaper[0][0], 'r')
### 代码结束 ###
期望输出
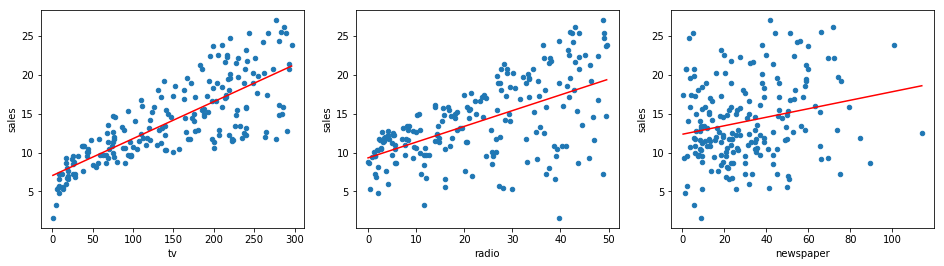
接下来,我们尝试建立包含全部特征的多元线性回归模型。
Exercise 9.3
挑战:使用 scikit-learn 提供的线性回归方法建立由 3 个特征与目标组成的多元线性回归模型。
规定:仅能使用 scikit-learn 提供的
sklearn.linear_model.LinearRegression
类。
from sklearn.linear_model import LinearRegression
## 代码开始 ### (≈ 4 行代码)
model = None
## 代码结束 ###
model.coef_, model.intercept_ # 返回模型自变量系数和截距项
参考答案 Exercise 9.3
from sklearn.linear_model import LinearRegression
### 代码开始 ### (≈ 4 行代码)
X = data[['tv', 'radio', 'newspaper']]
y = data.sales
model = LinearRegression()
model.fit(X, y)
### 代码结束 ###
model.coef_, model.intercept_ # 返回模型自变量系数和截距项
期望输出
(array([ 0.04576465, 0.18853002, -0.00103749]), 2.9388893694594067)
接下来,我们希望对多元线性回归模型进行检验。使用 statsmodels 库提供的相关方法来完成拟合优度检验和变量显著性检验。
Exercise 9.4
挑战:使用 statsmodels 库提供的相关方法来完成上面多元回归模型的拟合优度检验和变量显著性检验。
提示:你可以使用
statsmodels.api.sm.OLS
或
statsmodels.formula.api.smf,后一种实验未涉及,需自行了解学习。
import statsmodels.formula.api as smf
## 代码开始 ### (≈ 3 行代码)
results = None
## 代码结束 ###
results.summary2() # 输出模型摘要
参考答案 Exercise 9.4
import statsmodels.formula.api as smf
### 代码开始 ### (≈ 3 行代码)
results = smf.ols(formula='sales ~ tv + radio + newspaper', data=data).fit()
### 代码结束 ###
results.summary2() # 输出模型摘要
期望输出
我们可以看到,这里得到的回归拟合系数和上文 scikit-learn 计算结果一致。于此同时,tv 和 radio 的 P 值接近于 0 [精度],而 newspaper 的 P 值相对较大。我们可以认为 tv 和 radio 通过了变量显著性检验,而 newspaper 则未通过。实际上,你可以尝试去掉 newspaper 特征之后重新计算多元线性回归结果。
上面是去掉 newspaper 特征之后重新计算的结果,你可以发现包含和未包含 newspaper 的多元线性回归模型 \(R^2\) 值均为 0.896。这也就印证了该特征对于反映目标数值变化并无太大帮助。你可以尝试去除其余两个特征之一后,再查看 \(R^2\) 拟合优度值的变化。
○ 欢迎分享本文链接到你的社交账号、博客、论坛等。更多的外链会增加搜索引擎对本站收录的权重,从而让更多人看到这些内容。
