88. Python 微积分基础#
88.1. 介绍#
微积分是现代数学的基础,只要是机器学习算法必定需要进行公式推导,只要进行公式推导必定需要用到微积分。本实验首先从微积分的基础知识进行讲解,然后对梯度下降算法和最小二乘法的原理进行详细的阐述,最后利用这些算法完成了一个简单的最优化求解问题。本实验尝试以一种简单的方式来讲解微积分相关知识,对于每个知识点都附带了相关的例子,这些例子简单却能够很好的反应相关概念。因此,希望你能够静下心来仔细对其进行阅读和学习。
88.2. 知识点#
线性函数与非线性函数
导数与偏导数
链式法则
梯度下降算法
局部最优和全局最优
最小二乘法
函数是基础数学中最重要的理论之一。我们大概从很小的时候就开始学习函数以及它的基本性质了。因此,这里我们对那些了如指掌的性质不做解释,只阐述与机器学习相关的函数知识。
88.3. 函数的线性和非线性#
函数表示的是变量到变量之间的映射关系。
如果这种关系是一次函数,我们就称之为线性关系(又叫线性函数)。更加通俗的讲,如果两个变量分别作为点的横坐标和纵坐标,其图像是平面上的一条直线,则说明这两个变量的关系为线性关系。相反,图像不是一条直线,那么这种关系就被称之为非线性关系,如 指数函数、对数函数、幂函数等。
同理,在机器学习中,我们一般将能够使用线性函数解决的问题称之为线性问题。将必须使用非线性函数解决的问题称之为非线性问题。拿分类问题举例,如下图所示:

图一,我们可以使用一条直线将数据进行分类的问题就是线性问题,且我们把这条直线所在的函数称之为线性分类器。同理,类似于图二,需要使用曲线来完成分类的问题,我们称之为非线性问题,这条曲线也被叫做非线性分类器。
88.4. 导数#
函数值随着自变量的变化而变化,而这种变化的速率就是导数。函数 \(f(x)\) 的导数可以记作 \(f'(x)\),又可以记作 \(\frac{df}{dx}\)。导数衡量的,其实就是一个变量对函数值的影响能力。
导数值越大,则该变量每改变单位点对最终函数值的影响越大。且导数值为正时,代表自变量增大时函数值增大。反之,若导数值为负,则表示自变量增大时函数值减小。
常见的函数与导数对照如下:
|
原函数 \(f\) |
导函数 \(f'\) |
|---|---|
任何常数 |
0 |
|
\(x\) |
1 |
|
\(e ^ { x }\) |
\(e ^ { x }\) |
|
\(x ^ { 2 }\) |
2\(x\) |
|
\(\frac { 1 } { x }\) |
\(\frac { - 1 } { x ^ { 2 } }\) |
|
\(\ln ( x )\) |
\(\frac { 1 } { x }\) |
88.5. 偏导数#
上面我们列举的就是只有一个自变量的函数,如果自变量有多个,如何求导数呢?
比如对于函数 \(f = x + y\),怎样衡量 \(x\) 和 \(y\) 分别对函数值 \(f\) 的影响呢?为了解决这个问题,数学上引入了偏导的概念。
对一个多变量函数 \(f\),求 \(f\) 对其中一个自变量 \(x\) 的偏导很简单,就是 将与 \(x\) 无关的其他自变量视为常量 ,再进行单变量求导。得到的即为 \(f\) 对 \(x\) 的偏导。比如:
若存在函数 \(f=x+2y\), 则 \(f\) 对 \(x\) 求偏导的结果为 \(\frac{\partial f}{\partial x}=1\),对 \(y\) 求偏导的结果为 \(\frac{\partial f}{\partial y}=2\)。
若存在函数 \(f=x^2+2xy+y^2\),则 \(f\) 对 \(x\) 求偏导的结果为 \(\frac{\partial f}{\partial x}=2x+2y+0\),对 \(y\) 求偏导的结果为 \(\frac{\partial f}{\partial y}=0+2x+2y\)。
88.6. 梯度#
前面我们提到了,对于单变量函数来说,导数值的正负代表自变量对函数值影响的「方向」:变大或变小。
那么对于多变量函数来说,如何表达函数值的变化方向呢?这就引入了梯度的概念。梯度所表示的方向其实就是函数值 \(f\) 上升最快的方向。
梯度是一个向量,向量长度与自变量的个数相等。梯度是由每个自变量所对应的偏导值所组成的向量。如 \(f(x,y,z)\) 的梯度向量就是\((\frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z})\)。
对于函数 \(f=x^2+2xy+y^2\), 其梯度向量为 \((2x+2y,2x+2y)\)。对于具体的自变量的值,比如 \(x=1,y=1\) 的点,其梯度向量就为 \((4, 4)\)。又比如 \(x=10,y=-20\) 点,其梯度向量就为 \((-20,-20)\)。
我们可以把多变量函数中的梯度(每个变量的偏导数的组合)理解为单变量函数中的导数。
88.7. 链式法则#
像上面这样的「简单函数」的求导或者求偏导是较为简单的。而对于「复合函数」的求导,就需要用到一些新的知识了。比如下面这样的函数:
对于复合函数 \(y\) 关于 \(x\) 的求导,我们可以采用求导链式法则进行求导。
链式法则的形式如下:
我们先把 \(g(x)\) 看做整体,记作 \(u\)。因此 式子可以化为 \(y = f(u) = \frac{1}{u}\),进而得到:
由于 $\(u = e ^ { x }\)\( 因此:\)\(\frac{du}{dx}=e^x\)$
然后根据链式法则,我们可以得到:
这就是链式法则的全过程。在面对复合函数时,我们先把里面的函数看成一个整体,对外面的函数进行求导,然后再对里面的函数进行求导。这种像剥洋葱一样,一层一层的对当层变量函数进行求导,最后再把所有的导数相乘得到复函函数的导数的过程叫做链式法则。链式法则主要使用于神经网络的反向传播中。
88.8. 最优化理论#
88.9. 目标函数#
简单的说,目标函数就是整个问题的目标。机器学习中我们常常把预测值和真实值之间的距离作为我们的目标函数。该函数越小,则证明我们的模型的预测准确率越高。
模型训练其实就是利用相关算法求取目标函数最小值的过程。
为了方便讲解,我们可以引入一个简单的线性规划问题:一条长为 20 m 的铁丝被截成了两段,并将其分别弯成了两个正方形,要使两个正方形的面积和最小,两段铁丝的长度分别是多少?
设一段长为 \(x\),则另外一段长 \((20-x)\) 。那么我们可以根据上面点的描述,定义该问题的目标函数如下:
上面的函数 \(y\) 就是整个问题的目标函数。我们的目标就是求取 \(y\) 的最小值和最小值对应的 \(x\) 的值。
我们可以使用 Python 来定义一下这个函数 \(y\):
import math
def obj_fun(x):
s1 = math.pow(x/4, 2)
s2 = math.pow((20-x)/4, 2)
return s1+s2
obj_fun(x=5)
15.625
如上,我们定义了我们的目标函数
obj_fun,该函数可以根据上面公式计算任何
\(x\)
所对应的
\(y\)
值。得到目标函数之后,接下来我们就需要求取的该函数的最小值。那么如何求取该函数的最小值呢?这里我们使用梯度下降算法。
88.10. 梯度下降算法#
由于上面这个问题只是一个一元函数问题,我们可以简单的使用函数的求导法则,直接求出上面函数的最小值。而,使用梯度下降算法求解该问题未免有点「小题大做」。但是为了更好的入门该算法,我们就用这个比较简单的函数作为目标函数。
我们可以把梯度下降算法类比为一个下山的过程。假设一个人被困在山上,需要快速从山上下来,走到山底。 但是,由于山中浓雾很大,导致可视度很低。进而使我们无法确定下山的路径,只能看到周围的一些信息。也就是说我们需要走一步看一步再走一步再看一步。此时,我们就可以使用到梯度下降的算法,如下:
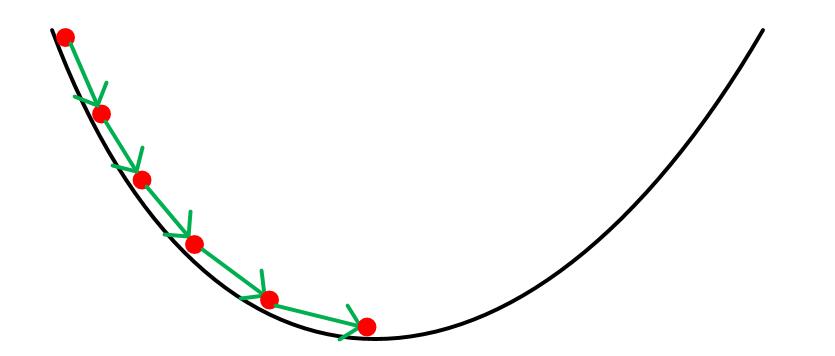
首先,以当前所在位置为基准,找到该位置周围最陡峭的方向,朝着该方向走一步。然后由以新的位置为基准,再次找最陡峭的方向,再朝着该方向走一步。如此循环,直到走到最低处为止。
而我们需要找的目标函数也可以看做一座山,我们的目标就是找到这座山的最小值,即山底。而上文提到的最陡峭的方向,也就是目标函数值下降最快的方向,也就是梯度的相反方向(梯度方向为函数值上升最快的方向)。
因此,为了寻找一个函数的最小值,我们需要利用当前位置计算梯度,然后根据梯度更新所在位置。然后再根据当前位置寻找梯度,再更新。如此循环,直到函数值最小。而根据梯度和当前位置更新下一次所在位置的数学表达式如下:
上面式子展示了函数 \(J(\theta)\) 的最小值的求解过程。
其中 \(\theta^0\) 表示当前所在位置,\(\theta^1\) 表示下一次的位置,\(\alpha\) 表示步长(即一次更新的距离),\(-\triangledown J(\theta^0)\) 表示 \(\theta^0\) 的梯度的相反方向。
为了方便计算,这里我们使用单变量函数进行举例。设函数 \(J(\theta)=\theta^2\)。由于单变量函数的梯度就是导数,因此 \(\triangledown J(\theta)=J'(\theta) = 2\theta\)。这里设置步长为 0.4,梯度下降的起点为 \(\theta^0=1\)。 接下来,我们利用梯度下降进行迭代:
如上所示,经过四次计算,我们的 \(J(\theta)\) 的值越来越小。如果迭代上千次,那么 \(J(\theta)\) 的值会逐渐接近于最小值。当然,可能永远无法与最小值相等,但是可以无限接近该值。
接下来,让我们回到计算铁丝所围成的两个正方形面积最小的求解上。函数还是如下:
通过计算,可以得到该函数的梯度为 \(y' = \frac{x}{4}-\frac{5}{2}\)。
让我们编写一下该函数的梯度函数代码:
def grad_fun(x):
# y' = x/4-5/2
return x/4-5/2
grad_fun(1)
-2.25
接下来,让我们使用梯度下降算法,求解 y 的最小值:
# 设置误差最小为 0.0001
# 即当函数下降距离已经小于 0.00000001 证明已经很接近最小值,无需继续迭代
e = 0.00000001
alpha = 1 # 设置步长
x = 1 # 设置初始位置
y0 = obj_fun(x)
ylists = [y0]
while(1):
gx = grad_fun(x)
# 梯度算法的核心公式
x = x - alpha*gx
y1 = obj_fun(x)
ylists.append(y1)
if(abs(y1-y0) < e):
break
y0 = y1
print("y 的最小值点", x)
print("y 的最小值", y1)
y 的最小值点 9.99971394602207
y 的最小值 12.50000001022836
从上面的结果我们可以看出,当 \(x\approx10\) 时,\(y\) 取得函数的最小值。
接下来,让我们来展示一下 \(y\) 的迭代过程:
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
plt.title("loss")
plt.plot(np.array(ylists))
plt.show()
如上图所示,我们通过梯度下降算法,求解了函数 y 的最小值。当然由于步长问题,可能我们找到的结果无法和正确答案完全一样(只能无限接近)。不过,通过这样的方法,我们能够很好的求得任何复杂函数的最小值点。
接下啦,让我们来求取一个复杂函数 \(f(x,y)= x^2+y^2-6x-4y+29\) 的最小值。
首先,编写函数 \(f(x,y)\):
def func(x, y):
return x**2+y**2-6*x-4*y+29
func(1, 1)
21
接下来,编写梯度的计算函数。由于有两个未知量,因此需要返回两个变量的偏导:
def grads(x, y):
# 计算x的偏导
dx = 2*x-6
dy = 2*y-4
return dx, dy
grads(1, 1)
(-4, -2)
接下来,让我们利用梯度下降算法计算该函数的最小值:
e = 0.00000001
alpha = 0.1
x = 1
y = 1
f0 = func(x, y)
flists = [f0]
while(1):
dx, dy = grads(x, y)
# 梯度算法的核心公式
x = x - alpha*dx
y = y - alpha*dy
f1 = func(x, y)
flists.append(f1)
if(abs(f1-f0) < e):
break
f0 = f1
print(f"f 的最小值点:x={x},y={y}")
print(f"f 的最小值 {f1}")
f 的最小值点:x=2.999891109642585,y=1.9999455548212925
f 的最小值 16.000000014821385
根据上面的结果,我们可以得到 \(x\approx3\) 和 \(y\approx2\) 时,原函数最小。
88.11. 局部最优和全局最优#
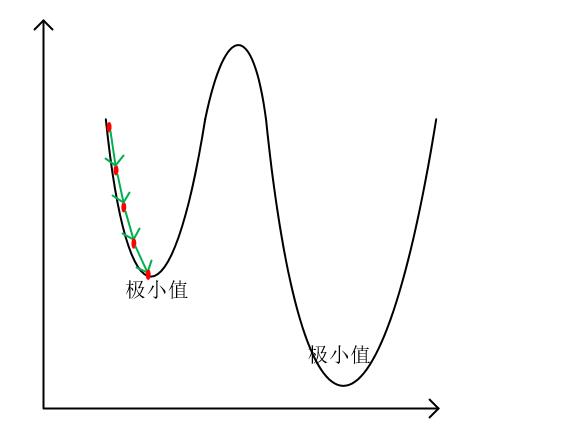
当然,梯度下降算法并不是每次都能求出一个函数的最小值的,如下所示:
从上图可以看出,我们使用梯度下降找到了该函数的一个极小值点,但是并没有找到真正的最小值点。
其实复杂函数中存在很多这样的极小值点,我们将这种在一定范围内的极小值点叫做局部最优点,并把这些极小值点中的最小值点称作全局最优点。
因此,为了能够保证我们找到的点尽可能是全局最优点,梯度下降的步长设置极为关键。我们可将步长设置的稍微大一点,这样,算法就能跨过极小值点两边的「峡谷」,进而找到真正的最小值点。当然,步长设置的过大,也可能让我们无法找到想要的答案。
其实很多机器学习问题都是一个非常复杂的函数的优化问题。这些函数往往存在大量的极值点和最值点。有时,我们确实很难分清我们找到的点是否为全局最优。同样,我们也没有证据证明我们的点是最小值点(除非我们利用穷举的方法列出所有的点)。
实际上,在机器学习中,我们很多时候,只能尽力的调节参数,找到一个较好的极小值点当做最值点。换句话说,很多时候,我们训练好的模型的解,其实仅仅是一个局部最优解。
这就像找另一半一样,我们永远不可能保证我们现在的另一半是最适合自己的。我们只是在森林中找到了一个局部最优解,但确实这个解是很多解中的不错的一个,我们就应当好好珍惜 TA。
88.12. 最小二乘法#
最小二乘法也是线性规划中最常用的理论之一。该方法主要用于拟合数据点,简单的说就是找到一条合适数据线(函数式)来表示所有数据的分布。假设我们需要使用该方法来拟合一元函数问题,我们就可以将问题进行如下描述:
假设存在 \(n\) 个数据点,其坐标为 \((x_1,y_1),(x_2,y_2),(x_3,y_3)...(x_n,y_n)\),我们需要使用函数 \(y=kx+b\) 来描述这些数据点的 \(y\) 坐标和 \(x\) 坐标之间的函数关系。这里,我们就可以使用最小二乘法来求取 \(k\) 和 \(b\) 的具体值。
首先让我们先来模拟一下这些数据集合,假设这些数据集合为 \(y=2x+3+(-1,1)\) 之间随机数。
x = [0]
y = [3]
for i in range(60):
xi = np.random.rand()*5
yi = 2*xi+3 + np.random.rand()*(-1)
x.append(xi)
y.append(yi)
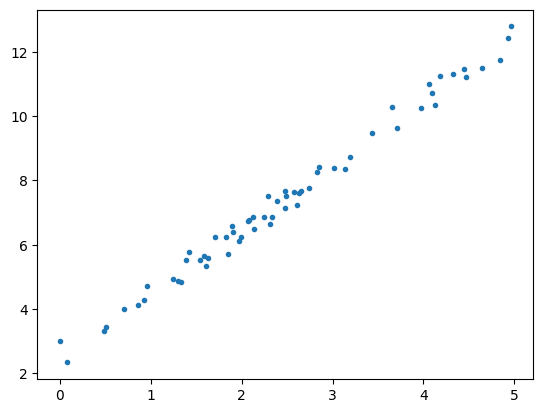
plt.plot(x, y, '.')
如上图所示,我们需要找到一条直线 \(y=kx+b\) 来衡量所有数据的分布。
那么怎样的直线才是最能表现数据分布的呢?当然,如果所有的数据点都能落在直线上,那么这条直线肯定是最佳的直线。但是实际生活中,不会存在这么理想的数据,一般数据的分布都会像上图一样,有趋势,但与直线不重合。
对于这种实际数据点,我们应该怎样找出一条最能反应分布的直线呢?最小二乘法给出了答案,该算法的核心思想就是「最小化误差平方和」。也就是说,如果我们找到的直线 \(y=kx+b\) 与所有数据点的距离和最小,那么该直线就为最佳拟合直线。
误差平方和的定义如下:
根据极值定理,当 \(f\) 取最小值或极小值时,\(f\) 所对应的点的斜率必定为 0,即未知数的导数为 0 。由于此时 \(k\) 和 \(b\) 是未知数,因此 \(f\) 关于 \(k\) 和 \(b\) 的偏导应当为 0。如下:
让我们将括号打开得到:
假设 \(A=\sum_{i=1}^n(x_i^2)\),\(B = \sum_{i=1}^n(x_i)\),\(C=\sum_{i=1}^n(x_iy_i)\),\(D=\sum_{i=1}^n(y_i)\),则上面式子可以代换为:
解上面的二元方程组可以得到:
由于数据据点已知,那么我们就可以很轻松的根据上面公式求出 \(k\) 和 \(b\) 的具体值。
上面的整个过程就是最小二乘法的全部过程。首先我们需要确定描述数据集的函数的形式,然后根据函数和数据集合,得到他们的误差平方和公式,然后利用最小二乘法求取公式中每个参数的具体值。
让我们利用最小二乘法对上面模拟的数据进行拟合,观察预测出来的 \(k\),\(b\) 的值与真实值之间的差距:
A = np.sum(np.multiply(x, x))
B = np.sum(x)
C = np.sum(np.multiply(x, y))
D = np.sum(y)
n = len(x)
k = (C*n-B*D)/(A*n-B*B)
b = (A*D-C*B)/(A*n-B*B)
print("实际的 k=2,b=3")
print("利用最小二乘法得到的 k = {},b={}".format(k, b))
实际的 k=2,b=3
利用最小二乘法得到的 k = 1.9970925836606068,b=2.469418590058912
当然,上面只是利用最小二乘法拟合了较为简单的一元函数。最小二乘法在拟合复杂的多元函数时,也可以产生不错的效果。但是由于公式的推导较为复杂,这里就不演示了。 如果有兴趣的话,你可以尝试一下,假设原函数的形式为 \(y=k_1x^2+k_2x+b\) 时,利用最小二乘法和数据点求得每个系数的具体取值。
88.13. 总结#
梯度下降算法是机器学习中使用最多的优化求解方法之一。为了方便讲解,本实验引用的例子较为简单,如果你想将这种算法理解的更加透彻,你可以尝试学习人工神经网络的相关知识进而了解梯度下降算法的高阶应用。
○ 欢迎分享本文链接到你的社交账号、博客、论坛等。更多的外链会增加搜索引擎对本站收录的权重,从而让更多人看到这些内容。