63. 生成对抗网络原理及构建#
63.1. 介绍#
本节实验我们将正式进入生成对抗网络(Generative Adversarial Nets,简称:GAN)的学习。Facebook AI 主要负责人 Yann LeCun 曾明确表示,生成对抗网络是近 10 年来机器学习领域最有趣的想法。不得不说,生成对抗网络已经成为了目前最火热的非监督深度学习的代表,也在整个工业界不断开发出它的新的应用。
63.2. 知识点#
生成对抗网络原理
生成对抗网络实现
生成对抗网络改进
生成对抗网络未来
63.3. 生成对抗网络原理#
生成对抗网络 是 2014年由伊恩·古德费洛等人提出的一种非监督式学习方法,该方法的特点是通过让两个神经网络相互博弈的方式进行学习。GAN 在图像生成方面很有优势,尤其是后期衍生出的 DCGAN,BiGAN,BigGAN 等。
在正式介绍生成对抗网络之前,首先我们来看一段有趣的对话:
男画家:哎,你看我画得好不好看? 女朋友:这是什么鬼,你不能把比例画得对称点吗? 男画家:哦,那我去改改。
男画家:这次你看我画的行不行,我把比例改对称了? 女朋友:呵呵,拜托你好好去学下怎么上色。 男画家:哦,那我去改改。
男画家:这次好点了吧,我上色很均匀了? 女朋友:呵呵,把你的画和梵大师的画摆一起,一看就看出差在哪里了。
男画家:这次呢,我练了很多次了? 女朋友:嗯,那我装裱起来了,就说是梵大师的真迹。
这就是一个男性画家在他女朋友这个最终决策标准下,依据梵大师作品的成长历程。其实,生成对抗网络就是按照这个原理搭建的,下面我们就来详细了解一下。
如下图所示,男画家就相当于生成器,能将一堆颜料、线条生成为一幅画(生成器输出,也是赝品)。他的女朋友在这里做为判别器,将真实的数据,也就是梵大师的作品,与之进行甄别。
整个对男画家的训练过程中,男画家的目的是让女朋友觉得他的作品与梵大师的无异。而女朋友为了训练他,就是要挑刺一样找出他的作品与梵大师作品的差异。最终,男画家的作品就能达到以假乱真的目的,那么他就完全成长了。在这个过程中,生成器和判别器一直处于对抗状态,这也就是生成对抗网络名字的起源。
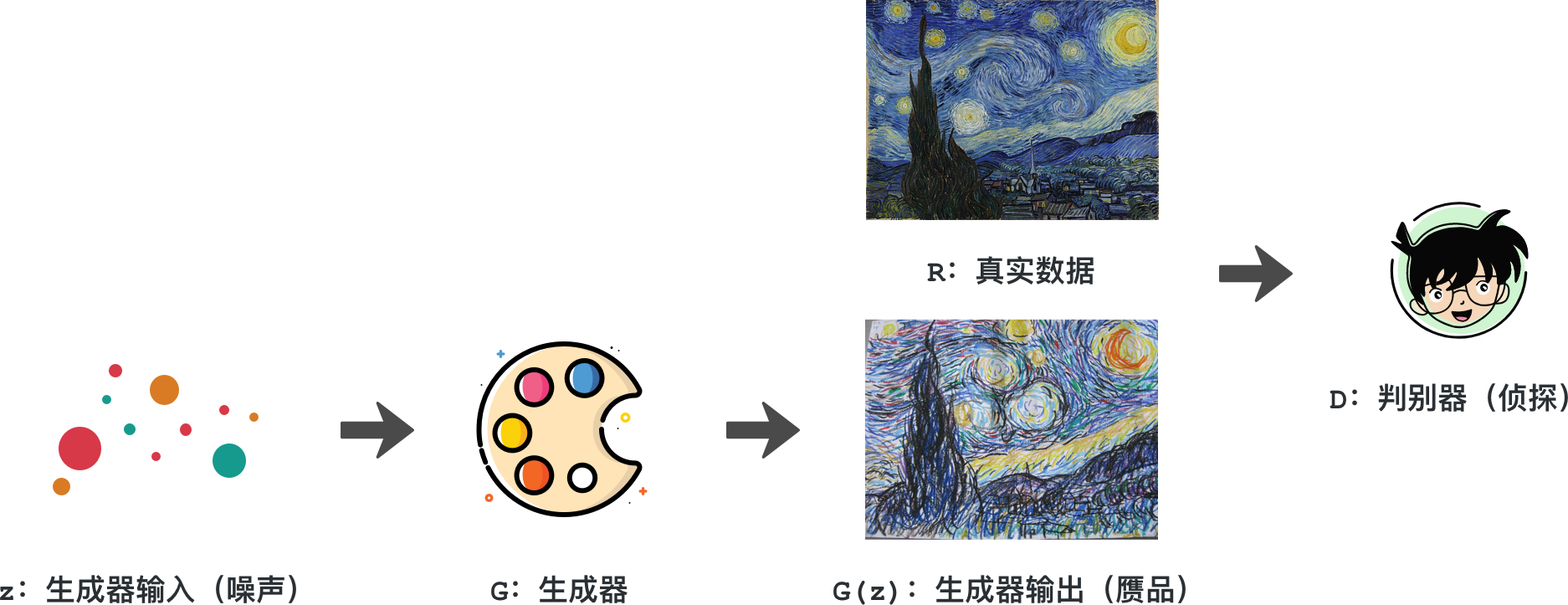
现在,我们把整个情节置换为神经网络。首先,通过对生成器输入一个分布的数据,生成器通过神经网络学着生成出一个输出(赝品),将之与真实的数据共同输入到判别器中。然后,判别器通过神经网络学着分辨两者的差异,做一个分类判断出这个作品是正品还是赝品。
这样,生成器不断训练为了以假乱真,判别器不断训练为了区分二者。最终,生成器真能完全模拟出与真实的数据一模一样的输出,判别器已经无力判断。基于伊恩·古德费洛最早对 GAN 的定义,GAN 实际上是在完成这样一个数学优化任务:
式中,\(G\) 表示生成器。\(D\) 表示判别器。\(V\) 是定义的价值函数,代表判别器的判别性能,该数值越大性能越好。\(p_{data}(x)\) 表示真实的数据分布,\(p_{z}(z)\) 表示生成器的输入数据分布,\(E\) 表示期望。
Note
下面公式解读部分需要一定的数学理论基础,如果无法理解可以跳过。
第一项 \(E_{p_{data}}\left ( x \right )[\log D(x)]\) 是依据真实数据的对数函数损失而构建的。具体可以理解为,最理想的情况是,判别器 \(D\) 能够对基于真实数据的分布数据给出 1 的判断。所以,通过优化 \(D\) 最大化这一项可以使 \(D(x)=1\)。其中,\(x\) 服从 \(p_{data}(x)\) 分布。
第二项,\(E_{p_{z}}\left ( z \right ) [\log (1-D(G(z))]\),是相对生成器的生成数据而言的。我们希望,当喂给判别器的数据是生成器的生成数据时,判别器能输出 0。由于 \(D\) 的输出是,输入数据是真实数据的概率,那么 \(1-D(输入)\) 是,输入数据是生成器生成数据的概率。通过优化 \(D\) 最大化这一项,则可以使 \(D(G(z))=0\)。其中,\(z\) 服从 \(p_{z}\) ,也就是生成器的生成数据分布。
那么对于生成器,我们优化什么呢?
生成器与判别器是对抗的关系,价值函数代表了判别器的判别性能。那么,通过优化 \(G\) 能够在第二项 \(E_{p_{z}}\left ( z \right ) [\log (1-D(G(z))]\) 上迷惑判别器,让判别器对于 \(G(z)\) 这个输入,尽可能地得到 \(D(G(z))=1\)。本质上,生成器就是在最小化这一项,也就是在最小化价值函数。
那么如何界定两个数据分布,也就是真实数据和生成器生成数据之间的差异呢?这里,需要引入 KL 散度的概念。
首先,可以证明,KL 散度具有非负性。同时也能发现,当且仅当 \(P\),\(Q\) 在离散型变量下是相同的分布时,即 \(p(x)=q(x)\) ,\(D_{KL}(P||Q)=0\)。KL 散度衡量了两个分布差异的程度,经常被视为两种分布间的距离。
但要注意的是,\(D_{KL}(P||Q)\neq D_{KL}(Q||P)\) ,即 KL 散度没有对称性。
接下来,将价值函数里的生成器固定不动,将期望写成积分的形式有:
整个式子中,只有一个变量 \(D\)。次数,对被积函数,令 \(y=D(x)\) ,\(a=p_{data}(x)\) ,\(b=p_{g}(x)\) ,\(a\),\(b\) 均为常数。那么,被积函数变为:
为了找到最优值 \(y\),需要对上式求一阶导数。而且,在 \(a+b\neq 0\) 的情况下有:
验证 \(f(y)\) 的二阶导数 \(f''(y)<0\),则 \(\frac{a}{a+b}\) 这个点为极大值,这个事实给出了最优判别器的存在可能性。
事实上,由于在实践中我们并不知道 \(a=p_{data}(x)\) ,也就是真实的数据的分布。那么,其实我们永远用不到这个式子去求解我们的最优判别性。但事实上,我们在利用深度学习训练判别器时,就是让 \(D\) 向这个目标逐渐逼近。
如果,最优的判别器如下:
我们将其代入 \(V(G,D)\) ,此时价值函数里只有 \(G\) 这一个变量:
此时,通过一个比较有技巧性地变换,我们可以得到下面的式子:
这个变换比较复杂,大家可以检验步与步之间的恒等性判断。根据对数的一些基本变换,可以得到:
最终得到:
因为 KL 散度的非负性,那么就可以知道 \(-\log4\) 就是 \(V(G)\) 的最小值,而且最小值是在当且仅当 \(p_{data}(x)=p_{g}(x)\) 时取得。这其实就是真实数据分布等于生成器的生成数据分布,可以从数学理论上证明了它的存在性和唯一性。
63.4. 生成对抗网络实现#
上面小节中,我们明确了 GAN 在优化什么样的函数,达到什么目的。但仅依据上面的理论证明,实践中会遇到一些问题需要对此做出改进后,才能投入实际实践过程。
生成器的输入:即上面的 \(p_{z}(z)\) ,我们当然不能让这个分布任意化,一般会设为常见的分布类型,如高斯分布、均匀分布等,然后生成器基于这个分布产生的数据生成自己的伪造数据来迷惑判别器。
期望如何模拟:实践中,我们是没有办法利用积分求数学期望的,所以一般只能从无穷的真实数据和无穷的生成器中采样以逼近真实的数学期望。
近似价值函数:若给定生成器 \(G\),并希望计算 \(maxV(G,D)\) 以求得判别器 \(D\)。那么,首先需要从真实的数据分布 \(p_{data}(x)\) 中采样 \(m\) 个样本 \({x^{1}, x^{2}, \dots, x^{m}}\)。并从生成器的输入,即 \(p_{z}(z)\) 中采样 \(m\) 个样本 \({\tilde{x}^{1}, \tilde{x}^{2}, \dots, \tilde{x}^{m}}\)。因此,最大化价值函数 \(V(G,D)\) 就可以使用以下表达式近似替代:
所以,可以把 GAN 的训练过程总结为:
-
从真实数据 \(p_{data}(x)\) 采样 \(m\) 个样本 \({x^{1},x^{2}...,x^{m}}\)。
-
从生成器的输入,即噪声数据 \(p_{z}(z)\) 采样 \(m\) 个样本 \({\tilde{x}^{1},\tilde{x}^{2},...,\tilde{x}^{m}}\)。
-
将噪声样本 \({\tilde{x}^{1}, \tilde{x}^{2}, ..., \tilde{x}^{m}}\) 投入到生成器中生成 \({G(\tilde{x}^{1}),G(\tilde{x}^{2}),...,G(\tilde{x}^{m})}\)。
-
通过梯度上升的方法,极大化价值函数,更新判别器的参数。
-
从生成器的输入,即噪声数据 \(p_{z}(z)\) 另外采样 \(m\) 个样本 \({z^{1},z^{2},...,z^{m}}\)。
-
将噪声样本 \({z^{1},z^{2},...,z^{m}}\) 投入到生成器中生成 \({G(z^{1}),G(z^{2}),...,G(z^{m})}\)。
-
通过梯度下降的方法,极小化价值函数,更新生成器的参数。
此时,你应该对 GAN 的训练过程有了初步的印象。接下来,我们用代码来加深认识,你会发现这样的训练会非常有趣。
首先,导入我们需要用到的模块。这里基于 PyTorch 搭建的 GAN,并完成一个手写识别网络数据的生成过程。其中,真实数据将利用 PyTorch 里面 MNIST 数据集。
import torch
from torchvision import datasets, transforms
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize(mean=[0.5], std=[0.5])
])
train_dataset = datasets.MNIST(root='.', train=True, download=True, transform=transform)
# 依旧采用 Mini-Batch 的训练方法,batch_size=128
dataloader = torch.utils.data.DataLoader(train_dataset, batch_size=64, shuffle=True)
dataloader
<torch.utils.data.dataloader.DataLoader at 0x1191f8280>
transform
函数允许我们把导入的数据集按照一定规则改变结构,我们在这里引入了
Normalize
将会把
Tensor
正则化。即:Normalized_image=(image-mean)/std。这样做的目的是便于后续的训练。代码最终生成了训练数据加载器。
数据准备完成。接下来,我们试着搭建深度学习模型,用于构建判别器和生成器。这里通过引入
nn.Module
基类的方法来搭建,学完前面的课程应该比较熟悉了。
import torch.nn as nn
class Discriminator(nn.Module):
# 判别器网络构建
def __init__(self):
super().__init__()
self.model = nn.Sequential(
nn.Linear(784, 1024),
nn.ReLU(),
nn.Dropout(0.3),
nn.Linear(1024, 512),
nn.ReLU(),
nn.Dropout(0.3),
nn.Linear(512, 256),
nn.ReLU(),
nn.Dropout(0.3),
nn.Linear(256, 1), # 最终输出为概率值
nn.Sigmoid()
)
def forward(self, x): # 判别器的前馈函数
out = self.model(x.reshape(x.size(0), 784)) # 数据展平传入全连接层
out = out.reshape(out.size(0), -1)
return out
判别器构建过程中,为了简化代码,我们将前面学习过的
nn.Module
和
nn.Sequential
融合在一起搭建。这样就可以避免在
forward
函数中把整个层与层的前向传播过程再写一遍。
网络使用了 4 层结构,并把每层都使用全连接配上 ReLU 激活再带上 Dropout 防止过拟合。最后一层,用 Sigmoid 保证输出值是一个 0 到 1 之间的概率值。设计前馈过程函数时,注意把每个样本大小 \(28\times28\) 的输入矩阵先转换为 784 的向量用于全连接。
接下来构建生成器。本模型中,我们设定生成器的每个输入样本是大小为 100 的向量,通过全连接层配上 ReLU 激活搭建,最后一层用 Tanh 激活,且保证每个样本输出是一个 784 的向量。
class Generator(nn.Module):
# 生成器网络构建
def __init__(self):
super().__init__()
self.model = nn.Sequential(
nn.Linear(100, 256),
nn.ReLU(),
nn.Linear(256, 512),
nn.ReLU(),
nn.Linear(512, 1024),
nn.ReLU(),
nn.Linear(1024, 784),
nn.Tanh()
)
def forward(self, x):
x = x.reshape(x.size(0), 100)
out = self.model(x)
return out
接下来,就是实例化生成器与判别器,设定学习率和损失函数。这里有个有趣的地方是,价值函数按照定义是:
PyTorch 中,BCELoss 表示二项 Cross Entropy,它的展开形式是:
其中 \(y\) 是 label,\(x\) 是输出。那么,对于 0 和 1 这两种 label 而言,当 \(y=0\),上式第一项不存在,就剩下 \(\tilde{V}\) 的第二项。当 \(y=1\),上式第二项不存在,就剩下 \(\tilde{V}\) 的第一项。那么 BCELoss 的结构就与损失函数 \(\tilde{V}\) 相同,只不过我们定义的损失函数有对真实数据与对生成器生成的数据两种情况的输出。
# 如果 GPU 可用则使用 CUDA 加速,否则使用 CPU 设备计算
dev = torch.device(
"cuda") if torch.cuda.is_available() else torch.device("cpu")
dev
device(type='cpu')
netD = Discriminator().to(dev)
netG = Generator().to(dev)
criterion = nn.BCELoss().to(dev)
lr = 0.0002 # 学习率
optimizerD = torch.optim.Adam(netD.parameters(), lr=lr) # Adam 优化器
optimizerG = torch.optim.Adam(netG.parameters(), lr=lr)
接下来,就可以定义如何训练判别器了。值得注意的是,这里需要设置
zero_grad()
来消除之前的梯度,以免造成梯度叠加。此外,我们通过将真实数据的损失和伪造数据的损失两部分相加,作为最终的损失函数。然后,通过后向传播,用之前的判定器优化器优化,通过降低
BCELoss 来增大价值函数的值。
def train_netD(netD, images, real_labels, fake_images, fake_labels):
netD.zero_grad()
outputs = netD(images) # 判别器输入真实数据
lossD_real = criterion(outputs, real_labels) # 计算损失
outputs = netD(fake_images) # 判别器输入伪造数据
lossD_fake = criterion(outputs, fake_labels) # 计算损失
lossD = lossD_real + lossD_fake # 损失相加
lossD.backward()
optimizerD.step()
return lossD
同样,接下来需要定义生成器的训练方法。注意,这里的 real_labels 在之后将设为 1。因为对于所有的生成器输出,我们希望它向真实的数据分布学习,那么 BCELoss 此时为 \(-\log x\)。最终,我们希望判别器的输出 \((x)\) 接近于 1,即判别器判断该数据为真实数据的概率越大。所以,这里依旧是在减少 BCELoss,则直接调用 criterion 就可以设定好生成器的损失函数。
def train_netG(netG, netD_outputs, real_labels):
netG.zero_grad()
lossG = criterion(netD_outputs, real_labels) # 判别器输出和真实数据之间的损失
lossG.backward()
optimizerG.step()
return lossG
一切准备就绪,就开始 GAN 的训练。按照之前的流程,在每一次的迭代中,首先应该训练判别器,然后训练生成器。调用之前创建的函数可以让这部分的代码非常清晰。
from IPython import display
import matplotlib.pyplot as plt
from torchvision.utils import make_grid
%matplotlib inline
# 设定一些参数方便训练代码书写
epochs = 100
for epoch in range(epochs):
for n, (images, _) in enumerate(dataloader): # Mini-batch 的训练方法,每次 100 个样本
fake_labels = torch.zeros([images.size(0), 1]).to(dev) # 伪造的数据 label 是 0
real_labels = torch.ones([images.size(0), 1]).to(dev) # 真实的数据 label 是 1
noise = torch.randn(images.size(0), 100).to(dev) # 产生生成器的输入,样本数*100 的矩阵
fake_images = netG(noise) # 通过生成器得到输出
lossD = train_netD(netD, images.to(dev), real_labels,
fake_images, fake_labels) # 训练判别器
noise = torch.randn(images.size(0), 100).to(dev) # 一组样本
fake_images = netG(noise) # 通过生成器得到这部分样本的输出
outputs = netD(fake_images) # 得到判别器对生成器的这部分数据的判定输出
lossG = train_netG(netG, outputs, real_labels) # 训练生成器
# 生成 64 组测试噪声样本,最终绘制 8x8 测试网格图像
fixed_noise = torch.randn(64, 100).to(dev)
# 为了使用 make_grid 绘图需要将数据处理成相应的形状
fixed_images = netG(fixed_noise).reshape([64, 1, 28, 28])
fixed_images = make_grid(fixed_images.data, nrow=8, normalize=True).cpu()
plt.figure(figsize=(6, 6))
plt.title("Epoch[{}/{}], Batch[{}/{}]".format(epoch+1, epochs, n+1, len(dataloader)))
plt.imshow(fixed_images.permute(1, 2, 0).numpy())
display.display(plt.gcf())
display.clear_output(wait=True)
上面的代码中,我们使用了
torchvision.utils.make_grid
🔗
将多张图像绘制在一起,PyTorch Tensor 具有的
permute
🔗
方法可以用来转换维度。整个代码的运行时间较长,生成器与判定器在不断博弈,所产生的图片也越来越逼真。下面是训练
100 个 Epoch 后生成的测试结果,可以看出已经是像模像样了。

63.5. 生成对抗网络改进#
上面的代码可能让你觉得十分兴奋,我们好像可以通过深度学习构建 GAN 来模仿好多好多事情。但是,相比起卷积神经网络擅长用于计算机视觉,循环神经网络擅长用于自然语言处理,GAN 尚且没有一个特别适合的应用场景。主要原因是 GAN 目前还存在诸多问题。例如:
-
不收敛问题:GAN 是两个神经网络之间的博弈。试想,如果判别器提前学到了非常强的,那么生成器很容易出现梯度消失而无法继续学习。所有 GAN 的收敛性一直是个问题,这样也导致 GAN 在实际搭建过程中对各种超参数都非常敏感,需要精心设计才能完成一次训练任务。
-
崩溃问题:GAN 模型被定义为一个极小极大问题,可以说,GAN 没有一个清晰的目标函数。这样会非常容易导致生成器在学习的过程中开始退化,总是生成相同的样本点,而这也进一步导致判别器总是被喂给相同的样本点而无法继续学习,整个模型崩溃。
-
模型过于自由: 理论上,我们希望 GAN 能够模拟出任意的真实数据分布,但事实上,由于我们没有对模型进行事先建模,再加上「真实分布与生成分布的样本空间并不完全重合」是一个极大概率事件。那么,对于较大的图片,如果像素一旦过多,GAN 就会变得越来越不可控,训练难度非常大。
但是,可能是因为 GAN 实在是太有趣了,近年来深度学习领域,关于 GAN 的研究是一浪高过一浪。不断有新的 GAN 的变式被提出,比如用 Wasserstein 距离来描述两个分布之间的距离,并依据 Wasserstein 距离设计了相应的算法,即 WGAN。
新的算法与原始 GAN 相比,参数更加不敏感,训练过程更加平滑。也有 CGAN 提出了一种带条件约束的 GAN,通过额外信息对模型增加限制条件,引导 GAN 去生成数据而避免崩溃问题。有兴趣的学员欢迎去阅读 GAN 的 相关论文。

上图展示了知名预印本论文站点 arXiv (读音如英语单词 archive)近年来 GAN 提交论文的数量变化情况,可见热度不断攀升。
63.6. 生成对抗网络未来#
深度学习在改变我们的世界,卷积神经网络主宰了计算机视觉领域,引领机器「看」得更清楚、更明白。循环神经网络引领着自然语言处理领域,我们的机器愈发智能化。但是 GAN 作为深度学习乃至整个机器学习这两年最火最潮流的话题,大家还不是特别清楚它究竟能运用到什么地方。可能的应用有:
-
扩充数据。就是指在训练数据不是很充裕的情况,利用 GAN 生成一些数据来辅助模型的训练。
-
图片生成,图像风格迁移,图像降噪修复,图像超分辨率,在这方面 GAN 已经有了一些良好的发现。
与强化学习结合,辅助智能机。
我们认为,GAN 已经给我们提供了一个解决很多问题的新的思路,就是把博弈论引入到机器学习过程中来。可以预见,GAN 本身的算法以及看问题的角度,必将对未来设计算法、以及解决实际问题产生深远的影响。可能以后 GAN 可以生成我们的语音,可以自己生成有我们出现的视频。脑洞更大点,GAN 或许也可以生成真实场景作为模拟器,帮助训练自动驾驶,甚至生成逼真的虚拟视觉给人们提供全新的游戏体验,这些种种有趣的想法有没有让你觉得好像看得到些许未来了呢。
也许盗梦空间离我们很近,也许盗梦空间的创造者就是你。
63.7. 总结#
本次实验对当下热门的 GAN 做了介绍,并尝试使用 PyTorch 训练一个生成手写字符的生成对抗网络。GAN 虽然有趣,但也面临着诸多问题,此次实验只是 GAN 的入门,而对 GAN 的深入研究是目前学术界正在做的事情。而你需要做到的是理解 GAN 的原理以及进一步熟悉 PyTorch 的使用。
相关链接
○ 欢迎分享本文链接到你的社交账号、博客、论坛等。更多的外链会增加搜索引擎对本站收录的权重,从而让更多人看到这些内容。
