Pro 会员计划

Pro 计划是作者为了维护和更新本教程而推出的会员计划，你可以获得更多的福利和服务，点击查看详情。

71. LSTM 预测股票价格#

71.1. 介绍#

股票交易走势预测是量化交易涉及的工作之一，即通过统计学和机器学习的手段来分析和预测价格走势情况。一般情况下，我们可以使用时间序列相关的建模方法，但本次挑战将尝试使用 LSTM 完成股票预测分析。

71.2. 知识点#

LSTM 网络构建
股票价格预测

相信每位股民都希望能预测股票价格，通过未卜先知的能力从股市中获利。由于影响股票价格变化的因素很多，且大多因素是无法量化，所以这是一件及其困难的事情。

不过，如果我们将股票历史数据看成时间序列，则可以通过统计学上的时间序列建模来分析趋势变化。除此之外，循环神经网络对于序列模型也有不错的表现，所以本次挑战将通过 LSTM 网络来预测股票价格走势。

首先，我们获取实时股票的交易数据。这里选择了 Quandl 金融数据模块。挑战需要先安装 Quandl 提供的 Python 库。

Note

pip install quandl

Quandl 未注册用户每天可以提交 50 次访问请求，注册账号则没有限制。本次实验使用课程提供的测试账号，如果自行使用请通过官网免费注册获取 API KEY。

                          import quandl

# 该 API KEY 仅限课程使用，其他用途请自行注册
quandl.ApiConfig.api_key = 'DdXEs2xFciyUXrER9-a7'
# 获取苹果公司股票数据
df_aapl = quandl.get('WIKI/AAPL')
df_aapl.head()

                        

	Open	High	Low	Close	Volume	Ex-Dividend	Split Ratio	Adj. Open	Adj. High	Adj. Low	Adj. Close	Adj. Volume
Date
1980-12-12	28.75	28.87	28.75	28.75	2093900.0	0.0	1.0	0.422706	0.424470	0.422706	0.422706	117258400.0
1980-12-15	27.38	27.38	27.25	27.25	785200.0	0.0	1.0	0.402563	0.402563	0.400652	0.400652	43971200.0
1980-12-16	25.37	25.37	25.25	25.25	472000.0	0.0	1.0	0.373010	0.373010	0.371246	0.371246	26432000.0
1980-12-17	25.87	26.00	25.87	25.87	385900.0	0.0	1.0	0.380362	0.382273	0.380362	0.380362	21610400.0
1980-12-18	26.63	26.75	26.63	26.63	327900.0	0.0	1.0	0.391536	0.393300	0.391536	0.391536	18362400.0

                          df_aapl.tail()

                        

	Open	High	Low	Close	Volume	Ex-Dividend	Split Ratio	Adj. Open	Adj. High	Adj. Low	Adj. Close	Adj. Volume
Date
2018-03-21	175.04	175.09	171.26	171.270	35247358.0	0.0	1.0	175.04	175.09	171.26	171.270	35247358.0
2018-03-22	170.00	172.68	168.60	168.845	41051076.0	0.0	1.0	170.00	172.68	168.60	168.845	41051076.0
2018-03-23	168.39	169.92	164.94	164.940	40248954.0	0.0	1.0	168.39	169.92	164.94	164.940	40248954.0
2018-03-26	168.07	173.10	166.44	172.770	36272617.0	0.0	1.0	168.07	173.10	166.44	172.770	36272617.0
2018-03-27	173.68	175.15	166.92	168.340	38962839.0	0.0	1.0	173.68	175.15	166.92	168.340	38962839.0

通过上面的代码，我们就可以加载出苹果公司上市以来的股票交易历史数据。由于实时数据需要付费订阅，所以我们只能获取到截止日期较早的免费数据。

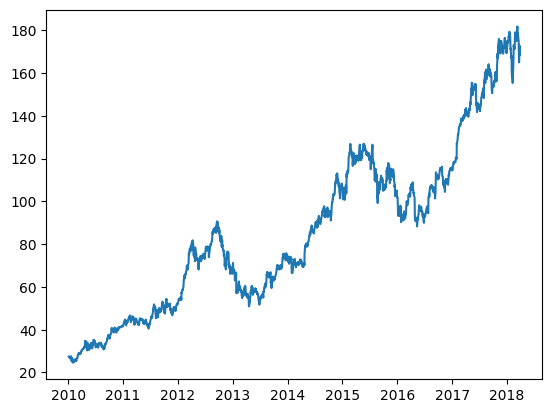
本次挑战只使用苹果公司 2010 年后的历史数据，并指定 Adj. Close 调整后的收盘价格为预测对象。下面，首先绘制出收盘价格的变化曲线。

                          from matplotlib import pyplot as plt
from pandas.plotting import register_matplotlib_converters
%matplotlib inline
register_matplotlib_converters()

df = df_aapl['2010':]["Adj. Close"]
plt.plot(df)

                        

[<matplotlib.lines.Line2D at 0x129465630>]

../_images/9b977359e5a29d0fc3f4bd18946dd30c1fa79821cf8a7e580d44e41dc0331ab1.png

然后，挑战将 2018 年之前的数据作为训练数据，2018 年之后的数据作为测试数据。同时，我们对数据进行归一化处理。

                          import numpy as np
from sklearn.preprocessing import MinMaxScaler

df_train = df[:'2018']  # 训练数据
df_test = df['2018':]  # 测试数据

scaler = MinMaxScaler(feature_range=(0, 1))  # 归一化
df_train_scaler = scaler.fit_transform(df_train.values.reshape(-1, 1))
df_test_scaler = scaler.transform(df_test.values.reshape(-1, 1))

df_train_scaler.shape, df_test_scaler.shape

                        

((2070, 1), (59, 1))

由于 MinMaxScaler 必须传入二维数组，所以上面使用 .reshape(-1, 1) 对数据进行形状转换。

接下来，我们需要设计实验方案。这里，我们采用今天预测明天的策略，时间间隔为 1 天。所以，需要将时间序列错位 1 天进行对应。

                          time_step = 1

train_t0 = df_train_scaler[:-time_step]  # 训练数据错位 1 天
train_t1 = df_train_scaler[time_step:]

test_t0 = df_test_scaler[:-time_step]
test_t1 = df_test_scaler[time_step:]

如上所示，t0 序列和 t1 序列对应时，时间错位 1 天。所以，我们可以使用 train_t0 作为网络的输入，而 train_t1 则作为目标值来训练 LSTM 网络。

Exercise 71.1

挑战：使用 TensorFlow Keras 顺序模型搭建方法构建 LSTM 模型。

规定：参考期望输出定义模型结构。

                          import tensorflow as tf

## 代码开始 ### (≈ 4 行代码)
model = None
## 代码结束 ###

参考答案 Exercise 71.1

                          import tensorflow as tf

### 代码开始 ### (≈ 4 行代码)
model = tf.keras.Sequential()
model.add(tf.keras.layers.LSTM(32, input_shape=(1, 1), return_sequences=True))
model.add(tf.keras.layers.LSTM(16))
model.add(tf.keras.layers.Dense(1))
### 代码结束 ###

                        

运行测试

                          model.summary()

                        

期望输出：

                      _________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
lstm_1 (LSTM)                (None, 1, 32)             4352      
_________________________________________________________________
lstm_2 (LSTM)                (None, 16)                3136      
_________________________________________________________________
dense_1 (Dense)              (None, 1)                 17        
=================================================================
Total params: 7,505
Trainable params: 7,505
Non-trainable params: 0
_________________________________________________________________

                    

接下来，编译并训练模型。

Exercise 71.2

挑战：编译并训练上面定义的 LSTM 模型。

规定：自由选择参数。

                          ## 代码开始 ### (≈ 2 行代码)

## 代码结束 ###

参考答案 Exercise 71.2

                          ### 代码开始 ### (≈ 2 行代码)
model.compile(loss='mse', optimizer='adam')
model.fit(np.atleast_3d(train_t0),
          train_t1.reshape(-1), epochs=5, batch_size=32)
### 代码结束 ###

                        

最后，使用 test_t0 进行测试，并计算其与 test_t1 之间的 MAPE 值。于此同时，挑战需要将真实数据变化曲线和预测结构变化曲线绘制在同一张图中进行对比。由于预测时使用的数据为归一化的结果，你可以使用 MinMaxScaler 提供的 inverse_transform 方法对数据进行还原处理。

Exercise 71.3

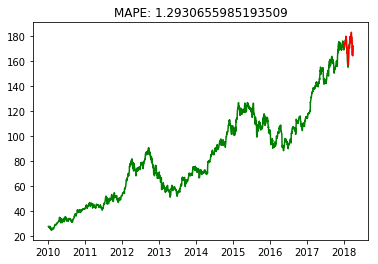
挑战：测试并绘制真实结果和预测结果的对比图像。

规定：真实结果以绿色线条展示，预测结果为红色线条，参考期望输出的样式。

                          ## 代码开始 ### (> 10 行代码)

## 代码结束 ###

参考答案 Exercise 71.3

                          test_pred = model.predict(np.atleast_3d(test_t0))  # 测试数据预测
test_pred = scaler.inverse_transform(test_pred)  # 数据还原

# 以原数据格式，对预测部分进行替换，训练部分数据设为 NAN 方便绘制到同一张图中
df_pred = df.copy()
df_pred[len(df_pred)-len(test_pred):] = test_pred.reshape(-1)
df_pred[:-len(test_pred)] = np.nan

# 计算 MAPE 结果
def mape(y_true, y_pred):
    n = len(y_true)
    mape = 100 * np.sum(np.abs((y_true-y_pred)/y_true)) / n
    return mape


y_true = df[len(df_pred)-len(test_pred):].values
y_pred = test_pred.reshape(-1)
mape = mape(y_true, y_pred)

plt.plot(df, 'g')
plt.plot(df_pred, 'r')
plt.title(f"MAPE: {mape}")

                        

期望输出：

○ 欢迎分享本文链接到你的社交账号、博客、论坛等。更多的外链会增加搜索引擎对本站收录的权重，从而让更多人看到这些内容。

如果你觉得这些内容对你有帮助，可以请我喝杯咖啡

70. 循环神经网络构建

72. 文本分类原理与实践