Pro 会员计划

Pro 计划是作者为了维护和更新本教程而推出的会员计划，你可以获得更多的福利和服务，点击查看详情。

51. TensorFlow 构建神经网络#

51.1. 介绍#

TensorFlow 作为深度学习框架，当然是为了帮助我们更便捷地构建神经网络。所以，本次实验将会了解如何使用 TensorFlow 来构建神经网络，并学会 TensorFlow 构建神经网络的重要函数和方法。

51.2. 知识点#

NumPy 构建神经网络
TensorFlow 构建神经网络
TensorFlow 完成 DIGITS 分类
TensorFlow 实现 Mini Batch 训练

前面的实验中，我们已经了解了 TensorFlow 的工作机制，并学会使用 TensorFlow 参与运算。TensorFlow 作为最出色的深度学习开源框架，在我看来主要有 2 点优势。第一是基于计算图的数值计算过程，最终目的是提升计算速度。其次就是对各种常用神经网络层进行封装，提高构建模型的速度。

所以，本次实验我们将了解如何使用 TensorFlow 构建神经网络。

51.3. NumPy 构建神经网络#

人工神经网络的实验中，我们使用 NumPy 构建简单的全连接神经网络。全连接指的是其每一个节点都与上一层每个节点相连。例如我们当时实现过的网络结构：

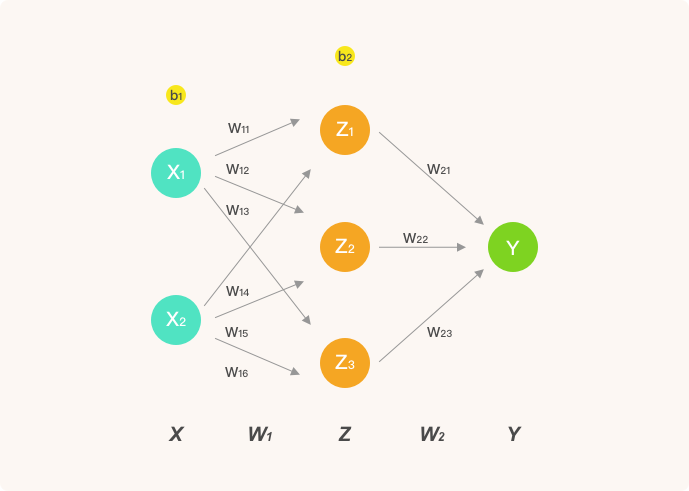
对于神经网络的实现，主要是前向传播和反向传播两个部分。前向传播当然是从输入 → 输出的计算，而反向传播则通过计算梯度来更新网络权重。这里，我们直接将前面感知机和人工神经网络实验中写过的代码拿过来使用。

                          import numpy as np


class NeuralNetwork:
    def __init__(self, X, y, lr):
        """初始化参数"""
        self.input_layer = X
        self.W1 = np.ones((self.input_layer.shape[1], 3))  # 初始化权重全为 1
        self.W2 = np.ones((3, 1))
        self.y = y
        self.lr = lr

    def forward(self):
        """前向传播"""
        self.hidden_layer = sigmoid(np.dot(self.input_layer, self.W1))
        self.output_layer = sigmoid(np.dot(self.hidden_layer, self.W2))
        return self.output_layer

    def backward(self):
        """反向传播"""
        d_W2 = np.dot(
            self.hidden_layer.T,
            (
                2
                * (self.output_layer - self.y)
                * sigmoid_derivative(np.dot(self.hidden_layer, self.W2))
            ),
        )

        d_W1 = np.dot(
            self.input_layer.T,
            (
                np.dot(
                    2
                    * (self.output_layer - self.y)
                    * sigmoid_derivative(np.dot(self.hidden_layer, self.W2)),
                    self.W2.T,
                )
                * sigmoid_derivative(np.dot(self.input_layer, self.W1))
            ),
        )

        # 参数更新
        self.W1 -= self.lr * d_W1
        self.W2 -= self.lr * d_W2

                        

下面，使用示例数据完成神经网络训练。

                          wget -nc https://cdn.aibydoing.com/aibydoing/files/course-12-data.csv

                        

                          import pandas as pd

# 直接运行加载数据集
df = pd.read_csv("course-12-data.csv", header=0)
df.head()  # 预览前 5 行数据

	X0	X1	Y
0	5.1	3.5	-1
1	4.9	3.0	-1
2	4.7	3.2	-1
3	4.6	3.1	-1
4	5.0	3.6	-1

                          from matplotlib import pyplot as plt

%matplotlib inline

X = df[["X0", "X1"]].values  # 输入值
y = df[["Y"]].values  # 真实 y
nn_model = NeuralNetwork(X, y, lr=0.001)  # 定义模型
loss_list = []  # 存放损失数值变化


def sigmoid(x):
    """激活函数"""
    return 1 / (1 + np.exp(-x))


def sigmoid_derivative(x):
    """sigmoid 函数求导"""
    return sigmoid(x) * (1 - sigmoid(x))


# 迭代 200 次
for _ in range(200):
    y_ = nn_model.forward()  # 前向传播
    nn_model.backward()  # 反向传播
    loss = np.square(np.subtract(y, y_)).mean()  # 计算 MSE 损失
    loss_list.append(loss)

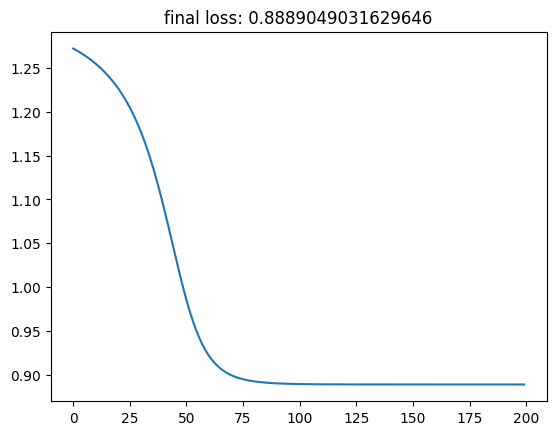
plt.plot(loss_list)  # 绘制 loss 曲线变化图
plt.title(f"final loss: {loss}")

                        

Text(0.5, 1.0, 'final loss: 0.8889049031629646')

../_images/c9774d32688e231ad233cfef5b63e1a19f77098bbeff51ec7cd2cb25cc583ba0.png

可以看到，仅包含 1 个隐含层的网络，使用 NumPy 实现的代码量就已不算少。深度神经网络中，可能会有数百层及数千个神经元，使用 NumPy 实现的复杂度可想而知。

51.4. TensorFlow 构建神经网络#

如果你仔细观察上面的代码，你就会发现随着神经网络的复杂程度增加，不仅代码量不断加大，最大的麻烦还在于求解梯度。所以，像 TensorFlow 等深度学习框架带来的最大便利在于，我们仅需要构建一个神经网络前向传播图，训练时就能够实现自动求导并更新参数。下面，我们就尝试使用 TensorFlow 的方式来重新构建上方包含 1 个隐含层的神经网络，并最终完成训练。

51.4.1. 处理张量数据#

首先，我们需要完成对输入数据特征和目标值的转换，将其全部转换为张量。

                            import tensorflow as tf

tf.get_logger().setLevel("ERROR")

# 将数组转换为常量张量
X = tf.cast(tf.constant(df[["X0", "X1"]].values), tf.float32)
y = tf.constant(df[["Y"]].values)

X.shape, y.shape

(TensorShape([150, 2]), TensorShape([150, 1]))

上面的代码中，tf.cast 主要用于转换张量类型为 tf.float32，这是为了和后面权重张量类型统一。通过输出可以看出，样本为 150 个，特征为 2 个，目标值 1 个。

51.4.2. 定义模型类#

接下来，我们就可以构建前向传播计算图了。这部分与 NumPy 构建前向传播过程非常相似，只是更换为使用 TensorFlow 构建。一般情况下，我们会将前向传播过程使用自定义模型类封装，并使用 TensorFlow 提供的 tf.Variable 随机初始化参数 \(W\)。

                            class Model(object):
    def __init__(self):
        # 初始化权重全为 1，也可以随机初始化
        # 选择变量张量，因为权重后续会不断迭代更新
        self.W1 = tf.Variable(tf.ones([2, 3]))
        self.W2 = tf.Variable(tf.ones([3, 1]))

    def __call__(self, x):
        hidden_layer = tf.nn.sigmoid(tf.linalg.matmul(x, self.W1))  # 隐含层前向传播
        y_ = tf.nn.sigmoid(tf.linalg.matmul(hidden_layer, self.W2))  # 输出层前向传播
        return y_

                          

上方展示了一个标准的 TensorFlow 模型类的构建方法，希望你能够对其留下印象，后面的复杂神经网络构建过程还会不断地使用这一结构。

我们可以实例化模型类，并传入输入数组进行简单测试。

                            model = Model()  # 实例化类
y_ = model(X)  # 测试输入
y_.shape  # 输出

                          

TensorShape([150, 1])

最终，我们得到了预测的输出，形状应该和数据集目标值一致，均为 \((150, 1)\)。

值得注意的是，上方构建网络的过程中，我们调用了 tf.nn 模块 🔗 下的 sigmoid 激活函数。tf.nn 是 TensorFlow 构建神经网络常用的模块，其包含封装好的神经网络层，激活函数，少量的损失函数或其他高阶 API 组件。

51.4.3. MSE 损失函数#

接下来，我们定义训练所需的损失函数。损失函数和 NumPy 构建时一样，这里选择平方和损失函数。其包含在 tf.losses 模块 🔗 下方。该模块包含一些比较基础的损失函数，例如这里用到的 MSE。

为了更方便后续调用，我们这里需要将 tf.losses.mean_squared_error MSE 损失函数计算方法封装成一个更完善的损失函数。特别地，将各样本损失使用 tf.reduce_mean 方法求和，得到样本总损失。

                            def loss_fn(model, X, y):
    y_ = model(X)  # 前向传播得到预测值
    # 使用 MSE 损失函数，并使用 reduce_mean 计算样本总损失
    loss = tf.reduce_mean(tf.losses.mean_squared_error(y_true=y, y_pred=y_))
    return loss

                          

同样，我们可以简单测试损失函数是否执行正常。

                            loss = loss_fn(model, X, y)
loss

<tf.Tensor: shape=(), dtype=float32, numpy=1.2723011>

51.4.4. 梯度下降优化迭代#

定义完损失函数，我们就可以使用梯度下降法来完成模型参数的迭代优化了。前面已经学习过了，TensorFlow 2 中的 Eager Execution 提供了 tf.GradientTape 用于追踪梯度，然后使用 tape.gradient 方法就可以计算梯度了。

                            EPOCHS = 200  # 迭代 200 次
LEARNING_RATE = 0.1  # 学习率

for epoch in range(EPOCHS):
    # 使用 GradientTape 追踪梯度
    with tf.GradientTape() as tape:
        loss = loss_fn(model, X, y)  # 计算 Loss，包含前向传播过程
    # 使用梯度下降法优化迭代
    # 输出模型需优化参数 W1，W2 自动微分结果
    dW1, dW2 = tape.gradient(loss, [model.W1, model.W2])
    model.W1.assign_sub(LEARNING_RATE * dW1)  # 更新梯度
    model.W2.assign_sub(LEARNING_RATE * dW2)

    # 每 100 个 Epoch 输出各项指标
    if epoch == 0:
        print(f"Epoch [000/{EPOCHS}], Loss: [{loss:.4f}]")
    elif (epoch + 1) % 100 == 0:
        print(f"Epoch [{epoch+1}/{EPOCHS}], Loss: [{loss:.4f}]")

                          

                            Epoch [000/200], Loss: [1.2723]
Epoch [100/200], Loss: [0.9051]
Epoch [200/200], Loss: [0.8889]

                          

值得注意的是，tape.gradient() 第二个参数支持以列表形式传入多个参数同时计算梯度。紧接着，使用 .assign_sub 即可完成公式中的减法操作用以更新梯度。你可以看到，损失函数的值随着迭代过程不断减小，意味着我们离最优化参数不断接近。

51.4.5. 使用 TensorFlow 优化器#

上面，我们手动构造了一个梯度下降迭代过程。实际应用中并不经常这样做，而是使用 TensorFlow 提供的现成优化器。你可以把优化器理解为对迭代优化过程的高阶封装，方便我们更快速完成模型迭代过程。

由于随机梯度下降远比普通梯度下降常用，所以 TensorFlow 没有提供普通梯度下降优化器。下面，我们选择随机梯度下降优化器对参数进行更新。优化器一般放在 tf.optimizers 模块 🔗 下方。

TensorFlow 优化器使用非常方便。如下所示，定义优化器并设定学习率。

                            # 定义 SGD 优化器，设定学习率，
optimizer = tf.optimizers.SGD(learning_rate=0.1)
optimizer

                          

<keras.src.optimizers.gradient_descent.SGD at 0x168011ab0>

然后，我们使用优化器替代上方的手动构建梯度下降过程。

                            loss_list = []  # 存放每一次 loss
model = Model()  # 实例化类
for epoch in range(EPOCHS):
    # 使用 GradientTape 追踪梯度
    with tf.GradientTape() as tape:
        loss = loss_fn(model, X, y)  # 计算 Loss，包含前向传播过程
        loss_list.append(loss)  # 保存每次迭代 loss

    grads = tape.gradient(loss, [model.W1, model.W2])  # 输出自动微分结果
    optimizer.apply_gradients(zip(grads, [model.W1, model.W2]))  # 使用优化器更新梯度

    # 每 100 个 Epoch 输出各项指标
    if epoch == 0:
        print(f"Epoch [000/{EPOCHS}], Loss: [{loss:.4f}]")
    elif (epoch + 1) % 100 == 0:
        print(f"Epoch [{epoch+1}/{EPOCHS}], Loss: [{loss:.4f}]")

                          

                            Epoch [000/200], Loss: [1.2723]
Epoch [100/200], Loss: [0.9051]
Epoch [200/200], Loss: [0.8889]

                          

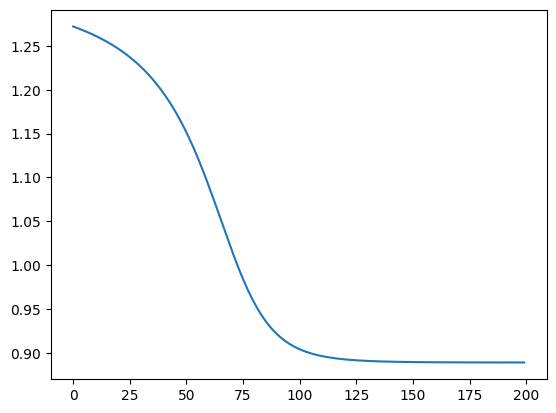
最后，可以将损失变化曲线绘制出来。

                            plt.plot(loss_list)  # 绘制 loss 变化图像

                          

[<matplotlib.lines.Line2D at 0x1264968f0>]

../_images/148ca4efa7a29e0a382e8d3264add55ba46fb5bda9d165f5e897a3577b7dbbf4.png

可以看到，我们就使用 TensorFlow 完成了一模一样的神经网络训练过程。最终，我们整理并精简上述使用 TensorFlow 构建简单神经网络的全部代码如下，你会发现相比于纯 NumPy 实现要简单清晰很多。

                        class Model(object):
    def __init__(self):
        self.W1 = tf.Variable(tf.ones([2, 3]))
        self.W2 = tf.Variable(tf.ones([3, 1]))

    def __call__(self, x):
        hidden_layer = tf.nn.sigmoid(tf.linalg.matmul(X, self.W1))
        y_ = tf.nn.sigmoid(tf.linalg.matmul(hidden_layer, self.W2))
        return y_

def loss_fn(model, X, y):
    y_ = model(X)
    loss = tf.reduce_mean(tf.losses.mean_squared_error(y_true=y, y_pred=y_))
    return loss

X = tf.cast(tf.constant(df[['X0', 'X1']].values), tf.float32)
y = tf.constant(df[['Y']].values)

model = Model()
EPOCHS = 200

for epoch in range(EPOCHS):
    with tf.GradientTape() as tape:
        loss = loss_fn(model, X, y)
    grads = tape.gradient(loss, [model.W1, model.W2])
    optimizer = tf.optimizers.SGD(learning_rate=0.1)
    optimizer.apply_gradients(zip(grads, [model.W1, model.W2]))

                      

下面，我们总结 NumPy 构建神经网络和使用 TensorFlow 构建神经网络的关键步骤：

NumPy 构建神经网络：定义数据 → 前向传播 → 手动推导梯度计算公式 → 反向传播 → 更新权重 → 迭代优化。
TensorFlow 构建神经网络：定义张量 → 定义前向传播模型 → 定义损失函数 → 定义优化器 → 迭代优化。

虽然，看起来二者步骤差不多。但是，TensorFlow 为我们省掉了推导反向传播更新参数的过程，这实际上是神经网络计算过程中最麻烦的事情。那你可能在想，这是怎么做得的呢？实际上，这就是得益于基于计算图的执行模式。当我们构建前向计算图时，TensorFlow 就能使用链式求导法则完成每一个节点的自动求导。详细可阅读 Automatic Differentiation。

除此之外，TensorFlow 对构建神经网络中的关键步骤都提供了封装好的 API，使用起来的复制程度也大大降低。在后面的实验中，我们会学习 Keras 等更高阶 API 的使用，难度将进一步降低。

51.5. DIGITS 分类#

DIGITS 手写字符数据集是机器学习中基础而经典的问题了，TensorFlow 构建神经网络的例子中，我们同样使用这个简单的数据集来练习。数据集加载和切分过程中，我们使用 scikit-learn 提供的 API 来完成。

                          from sklearn.datasets import load_digits

digits = load_digits()  # 读取数据

digits_X = digits.data  # 特征值
digits_y = digits.target  # 标签值

digits_X.shape, digits_y.shape

((1797, 64), (1797,))

51.5.1. 数据预处理#

首先，我们需要将目标值处理成独热编码的形式。独热编码在先前的内容中有过介绍，数据对应的目标是数字 0 ～ 9，处理成独热编码为：

0	→	0	0	0	0	0	0	0	0	0
1	→	1	0	0	0	0	0	0	0	0
2	→	0	1	0	0	0	0	0	0	0
3	→	0	0	1	0	0	0	0	0	0
4	→	0	0	0	1	0	0	0	0	0
5	→	0	0	0	0	1	0	0	0	0
6	→	0	0	0	0	0	1	0	0	0
7	→	0	0	0	0	0	0	1	0	0
8	→	0	0	0	0	0	0	0	1	0
9	→	0	0	0	0	0	0	0	0	1

处理成独热编码的原因会在后面进行说明。使用 NumPy 进行独热编码转换可以借助 np.eye 生成对角矩阵，然后在对应位置填充 1 来完成，这是一个处理的小技巧。

                            digits_y = np.eye(10)[digits_y.reshape(-1)]
digits_y

                            array([[1., 0., 0., ..., 0., 0., 0.],
       [0., 1., 0., ..., 0., 0., 0.],
       [0., 0., 1., ..., 0., 0., 0.],
       ...,
       [0., 0., 0., ..., 0., 1., 0.],
       [0., 0., 0., ..., 0., 0., 1.],
       [0., 0., 0., ..., 0., 1., 0.]])

                          

下面对数据进行切分。分为 80% 训练集和 20% 测试集。

                            from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(
    digits_X, digits_y, test_size=0.2, random_state=1
)

X_train.shape, X_test.shape, y_train.shape, y_test.shape

((1437, 64), (360, 64), (1437, 10), (360, 10))

这里我们不再提前将 NumPy 数组转换为 TensorFlow 张量，而是将数据转换步骤直接写在后续模型中。

51.5.2. 定义模型类#

我们拟构建的神经网络包含 2 个隐含层，结构如下：

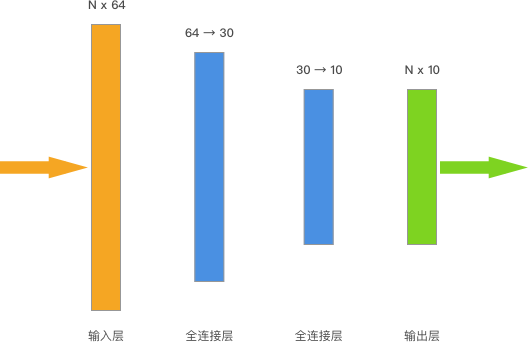
你可以看到，输入数据的 shape 是 \((N, 64)\)，N 代表样本数量。上面的神经网络一共有 2 个全连接层，其中第一层将输入数据处理成 \((N, 30)\)，接着第二个全连接层将训练数据处理成 \((N, 10)\)，最后直接作为输出层输出。而输出的 \((N, 10)\) 正好与独热编码的目标相互对应。

特别地，我们对隐含层进行 RELU 激活，输出层一般不激活。同时，这一次我们包含偏置项参数，并使用随机初始化张量参数。

                            import tensorflow as tf


class Model(object):
    def __init__(self):
        # 随机初始化张量参数
        self.W1 = tf.Variable(tf.random.normal([64, 30]))
        self.b1 = tf.Variable(tf.random.normal([30]))
        self.W2 = tf.Variable(tf.random.normal([30, 10]))
        self.b2 = tf.Variable(tf.random.normal([10]))

    def __call__(self, x):
        x = tf.cast(x, tf.float32)  # 转换输入数据类型
        # 线性计算 + RELU 激活
        fc1 = tf.nn.relu(tf.add(tf.matmul(x, self.W1), self.b1))  # 全连接层 1
        fc2 = tf.add(tf.matmul(fc1, self.W2), self.b2)  # 全连接层 2
        return fc2

                          

上面的模型类想必大家都很熟悉了。值得一提的是，tf.cast 不仅可以转换张量类型，还可以直接将 NumPy 数组转换为相应类型的常量张量，记住这一点使用时会非常方便。

51.5.3. 交叉熵损失函数#

完成前向传播模型构建后，下一个步骤是定义损失函数。这里，我们选择深度神经网络构建过程中十分常用的一个损失函数：交叉熵损失函数。交叉熵损失函数本质上就是我们前面学过的对数损失函数。交叉熵主要用于度量两个概率分布间的差异性信息，交叉熵损失函数会随着正确类别的概率不断降低，返回的损失值越来越大。交叉熵损失函数公式如下：

\[ H_{y^{\prime}}(y)=-\sum_{i} y_{i}^{\prime} \log \left(y_{i}\right) \]

其中，\(y_i\) 是预测的概率分布，而 \(y'_i\) 是实际的概率分布，也就是我们通过独热编码处理后的标签矩阵。

你可能会认为，那我们把上面最后一个全连接层的输出直接传入交叉熵损失函数，再求损失的极小值就可以了。逻辑正确，但是我们这里并不会直接把输出传进去，而是通过一个叫 Softmax 函数处理。

所以，介绍一下 Softmax 函数，一个非常漂亮且实用的函数。Softmax 函数公式如下，它可以将数值处理成概率。

\[ \operatorname{softmax}(x)_{i}=\frac{\exp \left(x_{i}\right)}{\sum_{j} \exp \left(x_{j}\right)} \]

简单来讲，我们可以将全连接层的输出通过该函数转换为概率，这在分类问题中经常用到。比如，你看到预测一个动物属于猫的概率为 95.8%，则很有可能是使用了 Softmax 函数。

例如，我们在鸢尾花分类问题中，如果最后全连接层给出了 3 个输出，分别是 -1.3，2.6，-0.9。通过 Softmax 函数处理之后，就可以得到 0.02，0.95，0.03 的概率值。也就是说有 95% 的概率属于 Versicolor 类别的鸢尾花。

来源

当然，这对于我们本次 DIGITS 的十分类问题同样适用，只是上面的 3 个分类看起来更简单而已。我们可以测试一下是不是上面的输出，下面实现 Softmax 函数并测试：

                            def softmax(x):
    # Softmax 实现
    exp_x = np.exp(x)
    return exp_x / np.sum(exp_x)

np.round(softmax([-1.3, 2.6, -0.9]), 2)

array([0.02, 0.95, 0.03])

所以说 Softmax 函数真的非常实用，在分类模型基本都可以看到它的身影。

为了便于使用，TensorFlow 中给出了交叉熵损失函数 + Softmax 函数二合一 API：tf.nn.softmax_cross_entropy_with_logits 🔗。下面我们就可以直接使用该函数，其中 logits 是模型输出，labels 为样本的真实值。该 API 会返回每个样本的损失计算结果，所以我们会使用 tf.reduce_mean 🔗 求得平均值，从而得到在训练集上的损失。

                            def loss_fn(model, x, y):
    preds = model(x)
    return tf.reduce_mean(
        tf.nn.softmax_cross_entropy_with_logits(logits=preds, labels=y)
    )

                          

回到之前留下的一个问题：为什么要对输出值进行独热编码？这就是因为我们会使用 Softmax 函数对全连接层输出进行概率处理，并最终计算交叉熵损失。而 tf.nn.softmax_cross_entropy_with_logits 自然就会要求传入独热编码数据了。

有了损失函数，接下来就是定义优化器求得全局损失的最小值了。这里我们不再使用梯度下降，而是深度学习中更为常用的 Adam 优化器。Adam 实际上就是一种数学优化方法，其最早由 Diederik P. Kingma 等于 2014 年提出 🔗。Adam 的全称为 Adaptive Moment Estimation，它是一种自适应学习率的算法，其针对每一个参数都计算自适应的学习率。

实验不再介绍 Adam 的数学优化过程，你可以直接通过 TensorFlow 调用 Adam 优化器。现在可以建立并开始执行神经网络迭代学习。

                            EPOCHS = 200  # 迭代此时
LEARNING_RATE = 0.02  # 学习率
model = Model()  # 实例化模型类
for epoch in range(EPOCHS):
    with tf.GradientTape() as tape:  # 追踪梯度
        loss = loss_fn(model, X_train, y_train)

    trainable_variables = [model.W1, model.b1, model.W2, model.b2]  # 需优化参数列表
    grads = tape.gradient(loss, trainable_variables)  # 计算梯度

    optimizer = tf.optimizers.Adam(learning_rate=LEARNING_RATE)  # Adam 优化器
    optimizer.apply_gradients(zip(grads, trainable_variables))  # 更新梯度

    # 每 100 个 Epoch 输出各项指标
    if epoch == 0:
        print(f"Epoch [000/{EPOCHS}], Loss: [{loss:.4f}]")
    elif (epoch + 1) % 100 == 0:
        print(f"Epoch [{epoch+1}/{EPOCHS}], Loss: [{loss:.4f}]")

                          

                            Epoch [000/200], Loss: [380.0146]
Epoch [100/200], Loss: [6.4553]
Epoch [200/200], Loss: [4.1002]

                          

至此，我们就按照标准 TensorFlow 构建神经网络步骤完成了 DIGITS 手写字符识别神经网络训练。

此时，你可能还有最后一个疑问，那就是想知道网络的表现如何，需要打印出网络的分类准确率。那么，这里就需要再定义一个准确度计算函数。首先 tf.math.argmax(y, 1) 🔗 从真实标签（独热编码）中返回张量轴上具有最大值的索引，从而将 Softmax 结果转换为对应的字符值。然后使用 tf.equal 比对各样本的结果是否正确，最终使用 reduce_mean 求得全部样本的分类准确度。

                            def accuracy_fn(logits, labels):
    preds = tf.argmax(logits, axis=1)  # 取值最大的索引，正好对应字符标签
    labels = tf.argmax(labels, axis=1)
    return tf.reduce_mean(tf.cast(tf.equal(preds, labels), tf.float32))

                          

下面我们重新执行训练过程，并打印出测试集上的分类准确率。

                            EPOCHS = 500  # 迭代此时
LEARNING_RATE = 0.02  # 学习率
model = Model()  # 实例化模型类
for epoch in range(EPOCHS):
    with tf.GradientTape() as tape:  # 追踪梯度
        loss = loss_fn(model, X_train, y_train)

    trainable_variables = [model.W1, model.b1, model.W2, model.b2]  # 需优化参数列表
    grads = tape.gradient(loss, trainable_variables)  # 计算梯度

    optimizer = tf.optimizers.Adam(learning_rate=LEARNING_RATE)  # Adam 优化器
    optimizer.apply_gradients(zip(grads, trainable_variables))  # 更新梯度

    accuracy = accuracy_fn(model(X_test), y_test)  # 计算准确度

    # 每 100 个 Epoch 输出各项指标
    if epoch == 0:
        print(f"Epoch [000/{EPOCHS}], Accuracy: [{accuracy:.2f}], Loss: [{loss:.4f}]")
    elif (epoch + 1) % 100 == 0:
        print(
            f"Epoch [{epoch+1}/{EPOCHS}], Accuracy: [{accuracy:.2f}], Loss: [{loss:.4f}]"
        )

                          

                            Epoch [000/500], Accuracy: [0.09], Loss: [412.3293]
Epoch [100/500], Accuracy: [0.88], Loss: [3.4343]
Epoch [200/500], Accuracy: [0.89], Loss: [2.0059]
Epoch [300/500], Accuracy: [0.91], Loss: [1.2532]
Epoch [400/500], Accuracy: [0.91], Loss: [0.9231]
Epoch [500/500], Accuracy: [0.91], Loss: [0.7796]

                          

可以看到，迭代 500 次后，测试集准确率大约在 95% 左右。（由于参数随机初始化，每次训练结果略有不同）

51.6. TensorFlow 实现 Mini Batch 训练#

你可能注意到了，上面我们在训练神经网络时，每一次都将全部的数据传入了网络中对参数进行优化。这样自然是最好的，但是当数据量太大时，矩阵计算就相当夸张了，占用的内存数甚至会导致完全无法训练。于是，在实践中往往会使用一种叫 Mini Batch 的方法，也就是将整个数据分成一些小批次放进模型里进行训练。

小批量实现的方法有很多，这里我们给出非常简单的一种。实验借助 scikit-learn 提供的 K 折交叉验证方法来将数据划分为 K 个 Mini Batch。简单来讲，我们可以通过 sklearn.model_selection.KFold 将数据划分为等间隔的 K 块，然后每次只选择 1 块数据传入，正好符合 Mini Batch 的思想了。

                          from sklearn.model_selection import KFold
from tqdm.notebook import tqdm

EPOCHS = 500  # 迭代此时
BATCH_SIZE = 64  # 每次迭代的批量大小
LEARNING_RATE = 0.02  # 学习率

model = Model()  # 实例化模型类

for epoch in tqdm(range(EPOCHS)):  # 设定全数据集迭代次数
    indices = np.arange(len(X_train))  # 生成训练数据长度规则序列
    np.random.shuffle(indices)  # 对索引序列进行打乱，保证为随机数据划分
    batch_num = int(len(X_train) / BATCH_SIZE)  # 根据批量大小求得要划分的 batch 数量
    kf = KFold(n_splits=batch_num)  # 将数据分割成 batch 数量份
    # KFold 划分打乱后的索引序列，然后依据序列序列从数据中抽取 batch 样本
    for _, index in kf.split(indices):
        X_batch = X_train[indices[index]]  # 按打乱后的序列取出数据
        y_batch = y_train[indices[index]]

        with tf.GradientTape() as tape:  # 追踪梯度
            loss = loss_fn(model, X_batch, y_batch)

        trainable_variables = [model.W1, model.b1, model.W2, model.b2]  # 需优化参数列表
        grads = tape.gradient(loss, trainable_variables)  # 计算梯度

        optimizer = tf.optimizers.Adam(learning_rate=LEARNING_RATE)  # Adam 优化器
        optimizer.apply_gradients(zip(grads, trainable_variables))  # 更新梯度
        accuracy = accuracy_fn(model(X_test), y_test)  # 计算准确度

    # 每 100 个 Epoch 输出各项指标
    if epoch == 0:
        print(f"Epoch [000/{EPOCHS}], Accuracy: [{accuracy:.2f}], Loss: [{loss:.4f}]")
    elif (epoch + 1) % 100 == 0:
        print(
            f"Epoch [{epoch+1}/{EPOCHS}], Accuracy: [{accuracy:.2f}], Loss: [{loss:.4f}]"
        )

                        

                          Epoch [000/500], Accuracy: [0.54], Loss: [23.4109]
Epoch [100/500], Accuracy: [0.94], Loss: [0.0000]
Epoch [200/500], Accuracy: [0.94], Loss: [0.0059]
Epoch [300/500], Accuracy: [0.95], Loss: [0.0000]
Epoch [400/500], Accuracy: [0.95], Loss: [0.0000]
Epoch [500/500], Accuracy: [0.95], Loss: [0.0000]

                        

上面的代码中，由于 KFold 循环得到的 index 永远是按顺序排列的，所以我们提前生成了数据长度的顺序序列 indices，然后使用 shuffle 打乱该序列。最后从打乱后的 indices 取出值作为训练数据取 Batch 的索引。

这样做的目的是，保证每一次 Epoch 迭代使用的 Mini Batch 的数据不同，且保证一个 Epoch 能轮巡完全部训练数据。可以看到，小批量迭代最终的准确率依旧不错，甚至会被完整数据集迭代还要好。后面还会学习到使用 TensorFlow 提供的 Mini Batch 方法来处理数据。

Note

实验中，我们使用 scikit-learn 提供的 K 折交叉验证来实现 TensorFlow 的小批量训练。该方法大家不必记忆，这只是为了教学演示，重点是看明白小批量训练的过程。大多数情况下，我们都不会自行实现小批量训练过程，而是直接使用 TensorFlow 高阶 API 中提供的方法。

上面的小例子中，出现了 2 个习惯性的叫法：Batch 和 Epoch，你会在后面经常看到。Batch 当然就是 Mini Batch，即每次从数据集中抽出一小部分用来训练神经网络。Epoch 则是将数据集完成训练多少次，Epoch 由有限个 Batch 组成。

关于 Batch 和 Epoch 的区别很多人容易混淆，你可以通过下方的示意图学会区分：

https://cdn.aibydoing.com/aibydoing/images/document-uid214893labid7506timestamp1555503487732.svg

除此之外，也可以阅读 Epoch vs Batch Size vs Iterations [需科学上网] 一文。

51.7. 总结#

本次实验中，我们学习了使用 TensorFlow 构建神经网络的经典方法和步骤，一定要熟记于心。实验中出现了多个常用的函数和类，都需要通过链接阅读官方文档深入了解。你可能会觉得，学了这么多感觉还不如使用 scikit-learn 提供的神经网络类简单。实际上，这只是学习 TensorFlow 构建神经网络的开始，后续我们会了解更为易用的高阶 API。除此之外，在深度神经网络的构建上，scikit-learn 是无法做到的，后面你就会清楚其只能使用 TensorFlow 等深度学习框架来完成。

0	→	0	0	0	0	0	0	0	0	0
1	→	1	0	0	0	0	0	0	0	0
2	→	0	1	0	0	0	0	0	0	0
3	→	0	0	1	0	0	0	0	0	0
4	→	0	0	0	1	0	0	0	0	0
5	→	0	0	0	0	1	0	0	0	0
6	→	0	0	0	0	0	1	0	0	0
7	→	0	0	0	0	0	0	1	0	0
8	→	0	0	0	0	0	0	0	1	0
9	→	0	0	0	0	0	0	0	0	1

0	→	0	0	0	0	0	0	0	0	0
1	→	1	0	0	0	0	0	0	0	0
2	→	0	1	0	0	0	0	0	0	0
3	→	0	0	1	0	0	0	0	0	0
4	→	0	0	0	1	0	0	0	0	0
5	→	0	0	0	0	1	0	0	0	0
6	→	0	0	0	0	0	1	0	0	0
7	→	0	0	0	0	0	0	1	0	0
8	→	0	0	0	0	0	0	0	1	0
9	→	0	0	0	0	0	0	0	0	1

0	→	0	0	0	0	0	0	0	0	0
1	→	1	0	0	0	0	0	0	0	0
2	→	0	1	0	0	0	0	0	0	0
3	→	0	0	1	0	0	0	0	0	0
4	→	0	0	0	1	0	0	0	0	0
5	→	0	0	0	0	1	0	0	0	0
6	→	0	0	0	0	0	1	0	0	0
7	→	0	0	0	0	0	0	1	0	0
8	→	0	0	0	0	0	0	0	1	0
9	→	0	0	0	0	0	0	0	0	1