91. NumPy 数值计算基础#
91.1. 介绍#
如果你使用 Python 语言进行科学计算,那么一定会接触到 NumPy。NumPy 是支持 Python 语言的数值计算扩充库,其拥有强大的多维数组处理与矩阵运算能力。除此之外,NumPy 还内建了大量的函数,方便你快速构建数学模型。
91.2. 知识点#
数值类型及多维数组
数组操作及随机抽样
数学函数及代数运算
数组索引及其他用法

NumPy 的英文全称为 Numerical Python,意味 Python 面向数值计算的第三方库。NumPy 的特点在于,针对 Python 内建的数组类型做了扩充,支持更高维度的数组和矩阵运算,以及更丰富的数学函数。
NumPy 是 Scipy.org 中最重要的库之一,它同时也被 Pandas,Matplotlib 等我们熟知的第三方库作为核心计算库。当你在单独安装这些库时,你会发现同时会安装 NumPy 作为依赖。
91.3. NumPy 数组类型#
我们先来了解 NumPy 支持的数据类型。Python
本身支持的数值类型有
int(整型,Python 2 中存在
long
长整型)、float(浮点型)、bool(布尔型) 和
complex(复数型)。
而 NumPy 支持比 Python 本身更为丰富的数值类型,细分如下:
类型 |
解释 |
|---|---|
bool |
布尔类型,1 个字节,值为 True 或 False。 |
int |
整数类型,通常为 int64 或 int32 。 |
intc |
与 C 里的 int 相同,通常为 int32 或 int64。 |
intp |
用于索引,通常为 int32 或 int64。 |
int8 |
字节(从 -128 到 127) |
int16 |
整数(从 -32768 到 32767) |
int32 |
整数(从 -2147483648 到 2147483647) |
int64 |
整数(从 -9223372036854775808 到 9223372036854775807) |
uint8 |
无符号整数(从 0 到 255) |
uint16 |
无符号整数(从 0 到 65535) |
uint32 |
无符号整数(从 0 到 4294967295) |
uint64 |
无符号整数(从 0 到 18446744073709551615) |
float |
float64 的简写。 |
float16 |
半精度浮点,5 位指数,10 位尾数 |
float32 |
单精度浮点,8 位指数,23 位尾数 |
float64 |
双精度浮点,11 位指数,52 位尾数 |
complex |
complex128 的简写。 |
complex64 |
复数,由两个 32 位浮点表示。 |
complex128 |
复数,由两个 64 位浮点表示。 |
在 NumPy 中,上面提到的这些数值类型都被归于
dtype(data-type)
对象的实例。 我们可以用
numpy.dtype(object,
align,
copy)
来指定数值类型。而在数组里面,可以用
dtype=
参数。
下面,我们就开始学习 NumPy,首先需要导入 NumPy。
import numpy as np # 导入 NumPy 模块
a = np.array([1.1, 2.2, 3.3], dtype=np.float64) # 指定 1 维数组的数值类型为 float64
a, a.dtype # 查看 a 及 dtype 类型
(array([1.1, 2.2, 3.3]), dtype('float64'))
你可以使用
.astype()
方法在不同的数值类型之间相互转换。
a.astype(int).dtype # 将 a 的数值类型从 float64 转换为 int,并查看 dtype 类型
dtype('int64')
91.4. NumPy 数组生成#
在 Python 内建对象中,数组有三种形式:
-
列表:
[1, 2, 3] -
元组:
(1, 2, 3, 4, 5) -
字典:
{A:1, B:2}
其中,元组与列表相似,不同之处在于元组的元素不能修改。而字典由键和值构成。python
标准类针对数组的处理局限于 1 维,并仅提供少量的功能。而
NumPy 最核心且最重要的一个特性就是
ndarray
多维数组对象,它区别于 Python
的标准类,拥有对高维数组的处理能力,这也是数值计算过程中缺一不可的重要特性。
NumPy 中,ndarray
类具有六个参数,它们分别为:
-
shape:数组的形状。 -
dtype:数据类型。 -
buffer:对象暴露缓冲区接口。 -
offset:数组数据的偏移量。 -
strides:数据步长。 -
order:{'C','F'},以行或列为主排列顺序。
下面,我们来了解创建 NumPy 多维数组的一些方法。在 NumPy 中,我们主要通过以下 5 种途径创建数组,它们分别是:
从 Python 数组结构列表,元组等转换。
-
使用
np.arange、np.ones、np.zeros等 NumPy 原生方法。 从存储空间读取数组。
通过使用字符串或缓冲区从原始字节创建数组。
-
使用特殊函数,如
random。
91.4.1. 列表或元组转换#
在 NumPy 中,我们使用
numpy.array
将列表或元组转换为
ndarray
数组。其方法为:
numpy.array(object, dtype=None, copy=True, order=None, subok=False, ndmin=0)
其中,参数:
-
object:列表、元组等。 -
dtype:数据类型。如果未给出,则类型为被保存对象所需的最小类型。 -
copy:布尔类型,默认 True,表示复制对象。 -
order:顺序。 -
subok:布尔类型,表示子类是否被传递。 -
ndmin:生成的数组应具有的最小维数。
下面,通过列表创建一个
ndarray
数组。
np.array([[1, 2, 3], [4, 5, 6]])
array([[1, 2, 3],
[4, 5, 6]])
或者是列表和元组。
np.array([(1, 2), (3, 4), (5, 6)])
array([[1, 2],
[3, 4],
[5, 6]])
91.4.2. arange
方法创建#
除了直接使用 array 方法创建
ndarray,在 NumPy
中还有一些方法可以创建一些有规律性的多维数。首先,我们来看一看
arange()。arange()
的功能是在给定区间内创建一系列均匀间隔的值。方法如下:
numpy.arange(start, stop, step, dtype=None)
你需要先设置值所在的区间
[开始,
停止),这是一个半开半闭区间。然后,在设置
step
步长用于设置值之间的间隔。最后的可选参数
dtype 可以设置返回ndarray
的值类型。
# 在区间 [3, 7) 中以 0.5 为步长新建数组
np.arange(3, 7, 0.5, dtype='float32')
array([3. , 3.5, 4. , 4.5, 5. , 5.5, 6. , 6.5], dtype=float32)
91.4.3. linspace
方法创建#
linspace 方法也可以像arange方法一样,创建数值有规律的数组。linspace
用于在指定的区间内返回间隔均匀的值。其方法如下:
numpy.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None)
-
start:序列的起始值。 -
stop:序列的结束值。 -
num:生成的样本数。默认值为50。 -
endpoint:布尔值,如果为真,则最后一个样本包含在序列内。 -
retstep:布尔值,如果为真,返回间距。 -
dtype:数组的类型。
np.linspace(0, 10, 10, endpoint=True)
array([ 0. , 1.11111111, 2.22222222, 3.33333333, 4.44444444,
5.55555556, 6.66666667, 7.77777778, 8.88888889, 10. ])
将
endpoint
参数改成
False
看看区别:
np.linspace(0, 10, 10, endpoint=False)
array([0., 1., 2., 3., 4., 5., 6., 7., 8., 9.])
91.4.4. ones
方法创建#
numpy.ones
用于快速创建数值全部为
1
的多维数组。其方法如下:
numpy.ones(shape, dtype=None, order='C')
其中:
-
shape:用于指定数组形状,例如(1, 2)或 3。 -
dtype:数据类型。 -
order:{'C','F'},按行或列方式储存数组。
np.ones((2, 3))
array([[1., 1., 1.],
[1., 1., 1.]])
91.4.5. zeros
方法创建#
zeros
方法和上面的
ones
方法非常相似,不同的地方在于,这里全部填充为
0。zeros
方法和
ones
是一致的。
numpy.zeros(shape, dtype=None, order='C')
其中:
-
shape:用于指定数组形状,例如(1, 2)或3。 -
dtype:数据类型。 -
order:{'C','F'},按行或列方式储存数组。
np.zeros((3, 2))
array([[0., 0.],
[0., 0.],
[0., 0.]])
91.4.6. eye
方法创建#
numpy.eye
用于创建一个二维数组,其特点是
k
对角线上的值为
1,其余值全部为
0。方法如下:
numpy.eye(N, M=None, k=0, dtype=<type 'float'>)
其中:
-
N:输出数组的行数。 -
M:输出数组的列数。 -
k:对角线索引:0(默认)是指主对角线,正值是指上对角线,负值是指下对角线。
np.eye(5, 4, 3)
array([[0., 0., 0., 1.],
[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]])
91.4.7. 从已知数据创建#
我们还可以从已知数据文件、函数中创建
ndarray。NumPy 提供了下面
5
个方法:
-
frombuffer(buffer):将缓冲区转换为1维数组。 -
fromfile(file,dtype,count,sep):从文本或二进制文件中构建多维数组。 -
fromfunction(function,shape):通过函数返回值来创建多维数组。 -
fromiter(iterable,dtype,count):从可迭代对象创建1维数组。 -
fromstring(string,dtype,count,sep):从字符串中创建1维数组。
np.fromfunction(lambda a, b: a + b, (5, 4))
array([[0., 1., 2., 3.],
[1., 2., 3., 4.],
[2., 3., 4., 5.],
[3., 4., 5., 6.],
[4., 5., 6., 7.]])
91.4.8. ndarray
数组属性#
首先,我们创建一个
ndarray
数组,首先,新建
a
并随意设定为一个 2 维数组。
a = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
a # 查看 a 的值
array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
ndarray.T
用于数组的转置,与
.transpose()
相同。
a.T
array([[1, 4, 7],
[2, 5, 8],
[3, 6, 9]])
ndarray.dtype
用来输出数组包含元素的数据类型。
a.dtype
dtype('int64')
ndarray.imag
用来输出数组包含元素的虚部。
a.imag
array([[0, 0, 0],
[0, 0, 0],
[0, 0, 0]])
ndarray.real用来输出数组包含元素的实部。
a.real
array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
ndarray.size用来输出数组中的总包含元素数。
a.size
9
ndarray.itemsize输出一个数组元素的字节数。
a.itemsize
8
ndarray.nbytes用来输出数组的元素总字节数。
a.nbytes
72
ndarray.ndim用来输出数组维度。
a.ndim
2
ndarray.shape用来输出数组形状。
a.shape
(3, 3)
ndarray.strides用来遍历数组时,输出每个维度中步进的字节数组。
a.strides
(24, 8)
91.5. 数组维度和形状#
前面,我们已经对 NumPy 数组的类型和常用的生成方法进行了介绍。再继续了解更多内容前,必须先搞清楚一个重要的问题,那就是 NumPy 数组的维度和形状。
NumPy 数组又被称之为
ndarray
多维数组,那么 n 就可以从 1 维依次递增。下图,我们展示了 1
至 3 维的 NumPy 数组示例。
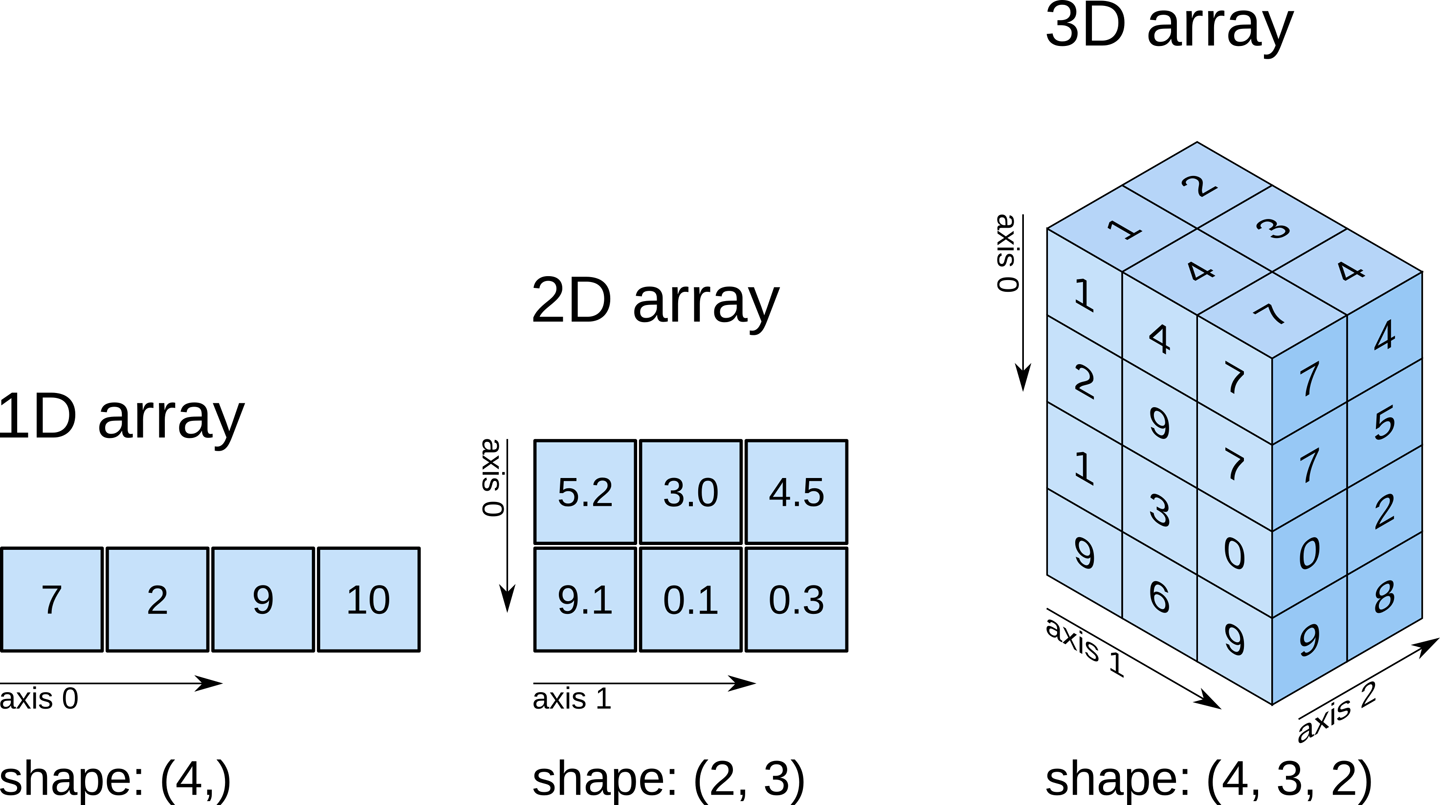
1 维数组可以被看作数学中的向量,2 维数组可以看作是矩阵,而 3 维数组则是一个数据立方。
接下来,我们尝试生成如图所示的示例数组。三维数组中部分数值无法从图示中获得,我们全部用 1 替代。
one = np.array([7, 2, 9, 10])
two = np.array([[5.2, 3.0, 4.5],
[9.1, 0.1, 0.3]])
three = np.array([[[1, 1], [1, 1], [1, 1]],
[[1, 1], [1, 1], [1, 1]],
[[1, 1], [1, 1], [1, 1]],
[[1, 1], [1, 1], [1, 1]]])
接下来,我们通过
.shape
属性查看 NumPy 数组的形状。
one.shape, two.shape, three.shape
((4,), (2, 3), (4, 3, 2))
你可以发现规律,.shape
得到的形状实际上是数组在每个轴 Axis 上面的元素数量,而
.shape
的长度的表明了数组的维度。
91.6. 数组基本操作#
至此,我们了解了如何利用 NumPy 创建各式各样的
ndarray,以及数组形状和维度的概念。接下来,我们将利用学会针对
ndarray
的各种花式操作技巧。
91.6.1. 重设形状#
reshape
可以在不改变数组数据的同时,改变数组的形状。其中,numpy.reshape()
等效于
ndarray.reshape()。reshape
方法非常简单:
numpy.reshape(a, newshape)
其中,a 表示原数组,newshape
用于指定新的形状(整数或者元组)。
np.arange(10).reshape((5, 2))
array([[0, 1],
[2, 3],
[4, 5],
[6, 7],
[8, 9]])
91.6.2. 数组展开#
ravel
的目的是将任意形状的数组扁平化,变为 1 维数组。ravel
方法如下:
numpy.ravel(a, order='C')
其中,a 表示需要处理的数组。order
表示变换时的读取顺序,默认是按照行依次读取,当
order='F'
时,可以按列依次读取排序。
a = np.arange(10).reshape((2, 5))
a
array([[0, 1, 2, 3, 4],
[5, 6, 7, 8, 9]])
np.ravel(a)
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
np.ravel(a, order='F')
array([0, 5, 1, 6, 2, 7, 3, 8, 4, 9])
91.6.3. 轴移动#
moveaxis
可以将数组的轴移动到新的位置。其方法如下:
numpy.moveaxis(a, source, destination)
其中:
-
a:数组。 -
source:要移动的轴的原始位置。 -
destination:要移动的轴的目标位置。
a = np.ones((1, 2, 3))
np.moveaxis(a, 0, -1)
array([[[1.],
[1.],
[1.]],
[[1.],
[1.],
[1.]]])
你可能没有看明白是什么意思,我们可以输出二者的
shape 属性:
a.shape, np.moveaxis(a, 0, -1).shape
((1, 2, 3), (2, 3, 1))
91.6.4. 轴交换#
和
moveaxis
不同的是,swapaxes
可以用来交换数组的轴。其方法如下:
numpy.swapaxes(a, axis1, axis2)
其中:
-
a:数组。 -
axis1:需要交换的轴 1 位置。 -
axis2:需要与轴 1 交换位置的轴 1 位置。
a = np.ones((1, 4, 3))
np.swapaxes(a, 0, 2)
array([[[1.],
[1.],
[1.],
[1.]],
[[1.],
[1.],
[1.],
[1.]],
[[1.],
[1.],
[1.],
[1.]]])
91.6.5. 数组转置#
transpose
类似于矩阵的转置,它可以将 2
维数组的横轴和纵轴交换。其方法如下:
numpy.transpose(a, axes=None)
其中:
-
a:数组。 -
axis:该值默认为none,表示转置。如果有值,那么则按照值替换轴。
a = np.arange(4).reshape(2, 2)
np.transpose(a)
array([[0, 2],
[1, 3]])
91.6.6. 维度改变#
atleast_xd
支持将输入数据直接视为
x 维。这里的
x
可以表示:1,2,3。方法分别为:
numpy.atleast_1d()
numpy.atleast_2d()
numpy.atleast_3d()
print(np.atleast_1d([1, 2, 3]))
print(np.atleast_2d([4, 5, 6]))
print(np.atleast_3d([7, 8, 9]))
[1 2 3]
[[4 5 6]]
[[[7]
[8]
[9]]]
91.6.7. 类型转换#
在 NumPy 中,还有一系列以 as
开头的方法,它们可以将特定输入转换为数组,亦可将数组转换为矩阵、标量,ndarray
等。如下:
-
asarray(a,dtype,order):将特定输入转换为数组。 -
asanyarray(a,dtype,order):将特定输入转换为ndarray。 -
asmatrix(data,dtype):将特定输入转换为矩阵。 -
asfarray(a,dtype):将特定输入转换为float类型的数组。 -
asarray_chkfinite(a,dtype,order):将特定输入转换为数组,检查NaN或infs。 -
asscalar(a):将大小为 1 的数组转换为标量。
这里以
asmatrix(data,dtype)
方法举例:
a = np.arange(4).reshape(2, 2)
np.asmatrix(a) # 将二维数组转化为矩阵类型
matrix([[0, 1],
[2, 3]])
91.6.8. 数组连接#
concatenate
可以将多个数组沿指定轴连接在一起。其方法为:
numpy.concatenate((a1, a2, ...), axis=0)
其中:
-
(a1, a2, ...):需要连接的数组。 -
axis:指定连接轴。
a = np.array([[1, 2], [3, 4], [5, 6]])
b = np.array([[7, 8], [9, 10]])
c = np.array([[11, 12]])
np.concatenate((a, b, c), axis=0)
array([[ 1, 2],
[ 3, 4],
[ 5, 6],
[ 7, 8],
[ 9, 10],
[11, 12]])
这里,我们可以尝试沿着横轴连接。但要保证连接处的维数一致,所以这里用到了
.T
转置。
a = np.array([[1, 2], [3, 4], [5, 6]])
b = np.array([[7, 8, 9]])
np.concatenate((a, b.T), axis=1)
array([[1, 2, 7],
[3, 4, 8],
[5, 6, 9]])
91.6.9. 数组堆叠#
在 NumPy 中,以下方法可用于数组的堆叠:
-
stack(arrays,axis):沿着新轴连接数组的序列。 -
column_stack():将 1 维数组作为列堆叠到 2 维数组中。 -
hstack():按水平方向堆叠数组。 -
vstack():按垂直方向堆叠数组。 -
dstack():按深度方向堆叠数组。
这里以
stack(arrays,axis)
方法举例:
a = np.array([1, 2, 3])
b = np.array([4, 5, 6])
np.stack((a, b))
array([[1, 2, 3],
[4, 5, 6]])
当然,也可以横着堆叠。
np.stack((a, b), axis=-1)
array([[1, 4],
[2, 5],
[3, 6]])
91.6.10. 拆分#
split
及与之相似的一系列方法主要是用于数组的拆分,列举如下:
-
split(ary,indices_or_sections,axis):将数组拆分为多个子数组。 -
dsplit(ary,indices_or_sections):按深度方向将数组拆分成多个子数组。 -
hsplit(ary,indices_or_sections):按水平方向将数组拆分成多个子数组。 -
vsplit(ary,indices_or_sections):按垂直方向将数组拆分成多个子数组。
下面,我们看一看
split
到底有什么效果:
a = np.arange(10)
np.split(a, 5)
[array([0, 1]), array([2, 3]), array([4, 5]), array([6, 7]), array([8, 9])]
除了 1 维数组,更高维度也是可以直接拆分的。例如,我们可以将下面的数组按行拆分为 2。
a = np.arange(10).reshape(2, 5)
np.split(a, 2)
[array([[0, 1, 2, 3, 4]]), array([[5, 6, 7, 8, 9]])]
NumPy 中还有针对数组元素添加或移除的一些方法。
91.6.11. 删除#
首先是
delete
删除:
-
delete(arr,obj,axis):沿特定轴删除数组中的子数组。
a = np.arange(12).reshape(3, 4)
np.delete(a, 2, 1)
array([[ 0, 1, 3],
[ 4, 5, 7],
[ 8, 9, 11]])
这里代表沿着横轴,将第 3 列(索引 2)删除。当然,你也可以沿着纵轴,将第三行删除。
np.delete(a, 2, 0)
array([[0, 1, 2, 3],
[4, 5, 6, 7]])
91.6.12. 数组插入#
再看一看
insert 插入,用法和
delete
很相似,只是需要在第三个参数位置设置需要插入的数组对象:
-
insert(arr,obj,values,axis):依据索引在特定轴之前插入值。
a = np.arange(12).reshape(3, 4)
b = np.arange(4)
np.insert(a, 2, b, 0)
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 0, 1, 2, 3],
[ 8, 9, 10, 11]])
91.6.13. 附加#
append
的用法也非常简单。只需要设置好需要附加的值和轴位置就好了。它其实相当于只能在末尾插入的
insert,所以少了一个指定索引的参数。
-
append(arr,values,axis):将值附加到数组的末尾,并返回 1 维数组。
a = np.arange(6).reshape(2, 3)
b = np.arange(3)
np.append(a, b)
array([0, 1, 2, 3, 4, 5, 0, 1, 2])
注意
append 方法返回值,默认是展平状态下的 1 维数组。
91.6.14. 重设尺寸#
resize
就很好理解了,直接举例子吧:
-
resize(a,new_shape):对数组尺寸进行重新设定。
a = np.arange(10)
a.resize(2, 5)
a
array([[0, 1, 2, 3, 4],
[5, 6, 7, 8, 9]])
你可能会纳闷了,这个
resize
看起来和上面的
reshape
一样呢,都是改变数组原有的形状。
其实,它们是有区别的,区别在于对原数组的影响。reshape
在改变形状时,不会影响原数组,相当于对原数组做了一份拷贝。而
resize
则是对原数组执行操作。
91.6.15. 翻转数组#
在 NumPy 中,我们还可以对数组进行翻转操作:
-
fliplr(m):左右翻转数组。 -
flipud(m):上下翻转数组。
a = np.arange(16).reshape(4, 4)
print(np.fliplr(a))
print(np.flipud(a))
[[ 3 2 1 0]
[ 7 6 5 4]
[11 10 9 8]
[15 14 13 12]]
[[12 13 14 15]
[ 8 9 10 11]
[ 4 5 6 7]
[ 0 1 2 3]]
91.6.16. NumPy 随机数#
NumPy 的随机数功能非常强大,主要由
numpy.random
模块完成。
首先,我们需要了解如何使用 NumPy 也就是生成一些满足基本需求的随机数据。主要由以下一些方法完成:
numpy.random.rand(d0,
d1,
...,
dn)
方法的作用为:指定一个数组,并使用
[0,
1)
区间随机数据填充,这些数据均匀分布。
np.random.rand(2, 5)
array([[0.81035309, 0.20557686, 0.37044025, 0.75564136, 0.89862485],
[0.7499761 , 0.38363492, 0.11483024, 0.22992515, 0.00490875]])
numpy.random.randn(d0,
d1,
...,
dn)
与
numpy.random.rand(d0,
d1,
...,
dn)
的区别在于,前者是从标准正态分布中返回一个或多个样本值。
np.random.randn(1, 10)
array([[ 0.02737128, -0.47012605, 0.8292128 , 0.23471071, 0.26814014,
1.13979343, -0.91319087, 0.85052568, 0.02528354, 0.01904666]])
randint(low,
high,
size,
dtype)
方法将会生成
[low,
high)
的随机整数。注意这是一个半开半闭区间。
np.random.randint(2, 5, 10)
array([2, 4, 2, 3, 2, 3, 2, 2, 2, 4])
random_sample(size)
方法将会在
[0,
1)
区间内生成指定
size
的随机浮点数。
np.random.random_sample([10])
array([0.36336217, 0.18256455, 0.51953106, 0.28146298, 0.58414531,
0.92387197, 0.7053034 , 0.04818513, 0.82172217, 0.86515322])
与
numpy.random.random_sample
类似的方法还有:
-
numpy.random.random([size]) -
numpy.random.ranf([size]) -
numpy.random.sample([size])
它们 4 个的效果都差不多。
choice(a,
size,
replace,
p)
方法将会给定的数组里随机抽取几个值,该方法类似于随机抽样。
np.random.choice(10, 5)
array([0, 9, 9, 6, 3])
上面的代码将会在
np.arange(10)
中随机抽取 5 个数。
91.6.17. 概率密度分布#
除了上面介绍的 6 种随机数生成方法,NumPy 还提供了大量的满足特定概率密度分布的样本生成方法。它们的使用方法和上面非常相似,这里就不再一一介绍了。列举如下:
-
numpy.random.beta(a,b,size):从 Beta 分布中生成随机数。 -
numpy.random.binomial(n, p, size):从二项分布中生成随机数。 -
numpy.random.chisquare(df,size):从卡方分布中生成随机数。 -
numpy.random.dirichlet(alpha,size):从 Dirichlet 分布中生成随机数。 -
numpy.random.exponential(scale,size):从指数分布中生成随机数。 -
numpy.random.f(dfnum,dfden,size):从 F 分布中生成随机数。 -
numpy.random.gamma(shape,scale,size):从 Gamma 分布中生成随机数。 -
numpy.random.geometric(p,size):从几何分布中生成随机数。 -
numpy.random.gumbel(loc,scale,size):从 Gumbel 分布中生成随机数。 -
numpy.random.hypergeometric(ngood, nbad, nsample, size):从超几何分布中生成随机数。 -
numpy.random.laplace(loc,scale,size):从拉普拉斯双指数分布中生成随机数。 -
numpy.random.logistic(loc,scale,size):从逻辑分布中生成随机数。 -
numpy.random.lognormal(mean,sigma,size):从对数正态分布中生成随机数。 -
numpy.random.logseries(p,size):从对数系列分布中生成随机数。 -
numpy.random.multinomial(n,pvals,size):从多项分布中生成随机数。 -
numpy.random.multivariate_normal(mean, cov, size):从多变量正态分布绘制随机样本。 -
numpy.random.negative_binomial(n, p, size):从负二项分布中生成随机数。 -
numpy.random.noncentral_chisquare(df,nonc,size):从非中心卡方分布中生成随机数。 -
numpy.random.noncentral_f(dfnum, dfden, nonc, size):从非中心 F 分布中抽取样本。 -
numpy.random.normal(loc,scale,size):从正态分布绘制随机样本。 -
numpy.random.pareto(a,size):从具有指定形状的 Pareto II 或 Lomax 分布中生成随机数。 -
numpy.random.poisson(lam,size):从泊松分布中生成随机数。 -
numpy.random.power(a,size):从具有正指数 a-1 的功率分布中在 0,1 中生成随机数。 -
numpy.random.rayleigh(scale,size):从瑞利分布中生成随机数。 -
numpy.random.standard_cauchy(size):从标准 Cauchy 分布中生成随机数。 -
numpy.random.standard_exponential(size):从标准指数分布中生成随机数。 -
numpy.random.standard_gamma(shape,size):从标准 Gamma 分布中生成随机数。 -
numpy.random.standard_normal(size):从标准正态分布中生成随机数。 -
numpy.random.standard_t(df,size):从具有 df 自由度的标准学生 t 分布中生成随机数。 -
numpy.random.triangular(left,mode,right,size):从三角分布中生成随机数。 -
numpy.random.uniform(low,high,size):从均匀分布中生成随机数。 -
numpy.random.vonmises(mu,kappa,size):从 von Mises 分布中生成随机数。 -
numpy.random.wald(mean,scale,size):从 Wald 或反高斯分布中生成随机数。 -
numpy.random.weibull(a,size):从威布尔分布中生成随机数。 -
numpy.random.zipf(a,size):从 Zipf 分布中生成随机数。
91.7. 数学函数#
使用 Python 自带的运算符,你可以完成数学中的加减乘除,以及取余、取整,幂次计算等。导入自带的 math 模块之后,里面又包含绝对值、阶乘、开平方等一些常用的数学函数。不过,这些函数仍然相对基础。如果要完成更加复杂一些的数学计算,就会显得捉襟见肘了。
NumPy 为我们提供了更多的数学函数,以帮助我们更好地完成一些数值计算。下面就依次来看一看。
91.7.1. 三角函数#
首先, 看一看 NumPy 提供的三角函数功能。这些方法有:
-
numpy.sin(x):三角正弦。 -
numpy.cos(x):三角余弦。 -
numpy.tan(x):三角正切。 -
numpy.arcsin(x):三角反正弦。 -
numpy.arccos(x):三角反余弦。 -
numpy.arctan(x):三角反正切。 -
numpy.hypot(x1,x2):直角三角形求斜边。 -
numpy.degrees(x):弧度转换为度。 -
numpy.radians(x):度转换为弧度。 -
numpy.deg2rad(x):度转换为弧度。 -
numpy.rad2deg(x):弧度转换为度。
比如,我们可以用上面提到的
numpy.rad2deg(x)
将弧度转换为度。
np.rad2deg(np.pi) # PI 值弧度表示
180.0
上面的这些函数非常简单,就不再一一举例了。你可以自己新建一些空白单元格练习。
91.7.2. 双曲函数#
在数学中,双曲函数是一类与常见的三角函数类似的函数。双曲函数经常出现于某些重要的线性微分方程的解中,使用 NumPy 计算它们的方法为:
-
numpy.sinh(x):双曲正弦。 -
numpy.cosh(x):双曲余弦。 -
numpy.tanh(x):双曲正切。 -
numpy.arcsinh(x):反双曲正弦。 -
numpy.arccosh(x):反双曲余弦。 -
numpy.arctanh(x):反双曲正切。
91.7.3. 数值修约#
数值修约, 又称数字修约, 是指在进行具体的数字运算前, 按照一定的规则确定一致的位数, 然后舍去某些数字后面多余的尾数的过程。比如, 我们常听到的「4 舍 5 入」就属于数值修约中的一种。
-
numpy.around(a):平均到给定的小数位数。 -
numpy.round_(a):将数组舍入到给定的小数位数。 -
numpy.rint(x):修约到最接近的整数。 -
numpy.fix(x, y):向 0 舍入到最接近的整数。 -
numpy.floor(x):返回输入的底部(标量 x 的底部是最大的整数 i)。 -
numpy.ceil(x):返回输入的上限(标量 x 的底部是最小的整数 i). -
numpy.trunc(x):返回输入的截断值。
随机选择几个浮点数,看一看上面方法的区别。
a = np.random.randn(5) # 生成 5 个随机数
a # 输出 a 的值
array([-0.91205945, 0.42692483, -2.27962497, 0.23174346, -0.09449969])
np.around(a)
array([-1., 0., -2., 0., -0.])
np.rint(a)
array([-1., 0., -2., 0., -0.])
np.fix(a)
array([-0., 0., -2., 0., -0.])
91.7.4. 求和、求积、差分#
下面这些方法用于数组内元素或数组间进行求和、求积以及进行差分。
-
numpy.prod(a, axis, dtype, keepdims):返回指定轴上的数组元素的乘积。 -
numpy.sum(a, axis, dtype, keepdims):返回指定轴上的数组元素的总和。 -
numpy.nanprod(a, axis, dtype, keepdims):返回指定轴上的数组元素的乘积, 将 NaN 视作 1。 -
numpy.nansum(a, axis, dtype, keepdims):返回指定轴上的数组元素的总和, 将 NaN 视作 0。 -
numpy.cumprod(a, axis, dtype):返回沿给定轴的元素的累积乘积。 -
numpy.cumsum(a, axis, dtype):返回沿给定轴的元素的累积总和。 -
numpy.nancumprod(a, axis, dtype):返回沿给定轴的元素的累积乘积, 将 NaN 视作 1。 -
numpy.nancumsum(a, axis, dtype):返回沿给定轴的元素的累积总和, 将 NaN 视作 0。 -
numpy.diff(a, n, axis):计算沿指定轴的第 n 个离散差分。 -
numpy.ediff1d(ary, to_end, to_begin):数组的连续元素之间的差异。 -
numpy.gradient(f):返回 N 维数组的梯度。 -
numpy.cross(a, b, axisa, axisb, axisc, axis):返回两个(数组)向量的叉积。 -
numpy.trapz(y, x, dx, axis):使用复合梯形规则沿给定轴积分。
下面,我们选取几个举例测试一下:
a = np.arange(10) # 生成 0-9
a # 输出 a 的值
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
np.sum(a)
45
np.diff(a)
array([1, 1, 1, 1, 1, 1, 1, 1, 1])
91.7.5. 指数和对数#
如果你需要进行指数或者对数求解,可以用到以下这些方法。
-
numpy.exp(x):计算输入数组中所有元素的指数。 -
numpy.log(x):计算自然对数。 -
numpy.log10(x):计算常用对数。 -
numpy.log2(x):计算二进制对数。
91.7.6. 算术运算#
当然,NumPy 也提供了一些用于算术运算的方法,使用起来会比 Python 提供的运算符灵活一些,主要是可以直接针对数组。
-
numpy.add(x1, x2):对应元素相加。 -
numpy.reciprocal(x):求倒数 1/x。 -
numpy.negative(x):求对应负数。 -
numpy.multiply(x1, x2):求解乘法。 -
numpy.divide(x1, x2):相除 x1/x2。 -
numpy.power(x1, x2):类似于 x1^x2。 -
numpy.subtract(x1, x2):减法。 -
numpy.fmod(x1, x2):返回除法的元素余项。 -
numpy.mod(x1, x2):返回余项。 -
numpy.modf(x1):返回数组的小数和整数部分。 -
numpy.remainder(x1, x2):返回除法余数。
a1 = np.random.randint(0, 10, 5) # 生成 5 个从 0-10 的随机整数
a2 = np.random.randint(0, 10, 5)
a1, a2 # 输出 a1, a2
(array([1, 5, 3, 6, 9]), array([5, 3, 1, 9, 4]))
np.add(a1, a2)
array([ 6, 8, 4, 15, 13])
np.negative(a1)
array([-1, -5, -3, -6, -9])
np.multiply(a1, a2)
array([ 5, 15, 3, 54, 36])
np.divide(a1, a2)
array([0.2 , 1.66666667, 3. , 0.66666667, 2.25 ])
np.power(a1, a2)
array([ 1, 125, 3, 10077696, 6561])
91.7.7. 矩阵和向量积#
求解向量、矩阵、张量的点积等同样是 NumPy 非常强大的地方。
-
numpy.dot(a, b):求解两个数组的点积。 -
numpy.vdot(a, b):求解两个向量的点积。 -
numpy.inner(a, b):求解两个数组的内积。 -
numpy.outer(a, b):求解两个向量的外积。 -
numpy.matmul(a, b):求解两个数组的矩阵乘积。 -
numpy.tensordot(a, b):求解张量点积。 -
numpy.kron(a, b):计算 Kronecker 乘积。
a = np.matrix([[1, 2, 3], [4, 5, 6]])
b = np.matrix([[2, 2], [3, 3], [4, 4]])
np.matmul(a, b)
matrix([[20, 20],
[47, 47]])
除了上面这些归好类别的方法,NumPy 中还有一些用于数学运算的方法,归纳如下:
-
numpy.angle(z, deg):返回复参数的角度。 -
numpy.real(val):返回数组元素的实部。 -
numpy.imag(val):返回数组元素的虚部。 -
numpy.conj(x):按元素方式返回共轭复数。 -
numpy.convolve(a, v, mode):返回线性卷积。 -
numpy.sqrt(x):平方根。 -
numpy.cbrt(x):立方根。 -
numpy.square(x):平方。 -
numpy.absolute(x):绝对值, 可求解复数。 -
numpy.fabs(x):绝对值。 -
numpy.sign(x):符号函数。 -
numpy.maximum(x1, x2):最大值。 -
numpy.minimum(x1, x2):最小值。 -
numpy.nan_to_num(x):用 0 替换 NaN。 -
numpy.interp(x, xp, fp, left, right, period):线性插值。
91.7.8. 代数运算#
上面,我们分为 8 个类别,介绍了 NumPy 中常用到的数学函数。这些方法让复杂的计算过程表达更为简单。除此之外,NumPy 中还包含一些代数运算的方法,尤其是涉及到矩阵的计算方法,求解特征值、特征向量、逆矩阵等,非常方便。
-
numpy.linalg.cholesky(a):Cholesky 分解。 -
numpy.linalg.qr(a ,mode):计算矩阵的 QR 因式分解。 -
numpy.linalg.svd(a ,full_matrices,compute_uv):奇异值分解。 -
numpy.linalg.eig(a):计算正方形数组的特征值和右特征向量。 -
numpy.linalg.eigh(a, UPLO):返回 Hermitian 或对称矩阵的特征值和特征向量。 -
numpy.linalg.eigvals(a):计算矩阵的特征值。 -
numpy.linalg.eigvalsh(a, UPLO):计算 Hermitian 或真实对称矩阵的特征值。 -
numpy.linalg.norm(x ,ord,axis,keepdims):计算矩阵或向量范数。 -
numpy.linalg.cond(x ,p):计算矩阵的条件数。 -
numpy.linalg.det(a):计算数组的行列式。 -
numpy.linalg.matrix_rank(M ,tol):使用奇异值分解方法返回秩。 -
numpy.linalg.slogdet(a):计算数组的行列式的符号和自然对数。 -
numpy.trace(a ,offset,axis1,axis2,dtype,out):沿数组的对角线返回总和。 -
numpy.linalg.solve(a, b):求解线性矩阵方程或线性标量方程组。 -
numpy.linalg.tensorsolve(a, b ,axes):为 x 解出张量方程 a x = b -
numpy.linalg.lstsq(a, b ,rcond):将最小二乘解返回到线性矩阵方程。 -
numpy.linalg.inv(a):计算逆矩阵。 -
numpy.linalg.pinv(a ,rcond):计算矩阵的(Moore-Penrose)伪逆。 -
numpy.linalg.tensorinv(a ,ind):计算 N 维数组的逆。
这里我们就不再一一尝试了,阅读一遍留下印象,用到时查阅官方文档即可。
91.8. 数组索引和切片#
我们已经明确了,Ndarray 是 NumPy 的组成核心,那么对于 NumPy
的多维数组,其实它完整集成了 Python 对于数组的索引语法
array[obj]。随着
obj
的不同,我们可以实现字段访问、数组切片、以及其他高级索引功能。
91.8.1. 数组索引#
我们可以通过索引值(从 0 开始)来访问 Ndarray 中的特定位置元素。NumPy 中的索引和 Python 对 list 索引的方式非常相似,但又有所不同。我们一起来看一下:
首先是,一维数据索引:
a = np.arange(10) # 生成 0-9
a
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
获取索引值为 1 的数据。
a[1]
1
分别获取索引值为 1,2,3 的数据。
a[[1, 2, 3]]
array([1, 2, 3])
对于二维数据而言:
a = np.arange(20).reshape(4, 5)
a
array([[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14],
[15, 16, 17, 18, 19]])
获取第 2 行,第 3 列的数据。
a[1, 2]
7
如果,我们使用 Python 中的 list 索引同样的值,看看有什么区别:
a = a.tolist()
a
[[0, 1, 2, 3, 4], [5, 6, 7, 8, 9], [10, 11, 12, 13, 14], [15, 16, 17, 18, 19]]
按照上面的方法获取第 2 行,第 3 列的数据。【报错】
a[1, 2]
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
Cell In[73], line 1
----> 1 a[1, 2]
TypeError: list indices must be integers or slices, not tuple
Python 中 list 索引 2 维数据的方法正确的做法是:
a[1][2]
7
如何索引二维 Ndarray 中的多个元素值,这里使用逗号,分割:
a = np.arange(20).reshape(4, 5)
a
array([[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14],
[15, 16, 17, 18, 19]])
a[[1, 2], [3, 4]]
array([ 8, 14])
这里需要注意索引的对应关系。我们实际获取的是
[1,
3],也就是第
2
行和第
4
列对于的值
8。以及
[2,
4],也就是第
3
行和第
5
列对应的值
14。
那么,三维数据呢?
a = np.arange(30).reshape(2, 5, 3)
a
array([[[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8],
[ 9, 10, 11],
[12, 13, 14]],
[[15, 16, 17],
[18, 19, 20],
[21, 22, 23],
[24, 25, 26],
[27, 28, 29]]])
a[[0, 1], [1, 2], [1, 2]]
array([ 4, 23])
91.8.2. 数组切片#
NumPy 里面针对Ndarray的数组切片和 Python 里的
list
切片操作是一样的。其语法为:
Ndarray[start:stop:step]
[start:stop:step]
分别代表
[起始索引:截至索引:步长]。对于一维数组:
a = np.arange(10)
a
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
a[:5]
array([0, 1, 2, 3, 4])
a[5:10]
array([5, 6, 7, 8, 9])
a[0:10:2]
array([0, 2, 4, 6, 8])
对于多维数组,我们只需要用逗号
,
分割不同维度即可:
a = np.arange(20).reshape(4, 5)
a
array([[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14],
[15, 16, 17, 18, 19]])
先取第 3,4 列(第一个维度),再取第 1,2,3 行(第二个维度)
a[0:3, 2:4]
array([[ 2, 3],
[ 7, 8],
[12, 13]])
按步长为 2 取所有列和所有行的数据。
a[:, ::2]
array([[ 0, 2, 4],
[ 5, 7, 9],
[10, 12, 14],
[15, 17, 19]])
当超过 3 维或更多维时,用 2 维数据的切片方式类推即可。
91.8.3. 排序、搜索、计数#
最后,再介绍几个 NumPy 针对数组元素的使用方法,分别是排序、搜索和计数。
我们可以使用
numpy.sort 方法对多维数组元素进行排序。其方法为:
numpy.sort(a, axis=-1, kind='quicksort', order=None)
其中:
-
a:数组。 -
axis:要排序的轴。如果为None,则在排序之前将数组铺平。默认值为-1,沿最后一个轴排序。 -
kind:{'quicksort','mergesort','heapsort'},排序算法。默认值为quicksort。
举个例子:
a = np.random.rand(20).reshape(4, 5)
a
array([[0.43755025, 0.2309869 , 0.1190329 , 0.4704277 , 0.35403564],
[0.95299435, 0.78530024, 0.42953847, 0.96155494, 0.62215496],
[0.45888738, 0.34246414, 0.72236349, 0.56836218, 0.28036395],
[0.59394576, 0.6396651 , 0.66637642, 0.18451326, 0.98310221]])
np.sort(a)
array([[0.1190329 , 0.2309869 , 0.35403564, 0.43755025, 0.4704277 ],
[0.42953847, 0.62215496, 0.78530024, 0.95299435, 0.96155494],
[0.28036395, 0.34246414, 0.45888738, 0.56836218, 0.72236349],
[0.18451326, 0.59394576, 0.6396651 , 0.66637642, 0.98310221]])
除了
numpy.sort,还有这样一些对数组进行排序的方法:
-
numpy.lexsort(keys ,axis):使用多个键进行间接排序。 -
numpy.argsort(a ,axis,kind,order):沿给定轴执行间接排序。 -
numpy.msort(a):沿第 1 个轴排序。 -
numpy.sort_complex(a):针对复数排序。
91.8.4. 搜索和计数#
除了排序,我们可以通过下面这些方法对数组中元素进行搜索和计数。列举如下:
-
argmax(a ,axis,out):返回数组中指定轴的最大值的索引。 -
nanargmax(a ,axis):返回数组中指定轴的最大值的索引,忽略 NaN。 -
argmin(a ,axis,out):返回数组中指定轴的最小值的索引。 -
nanargmin(a ,axis):返回数组中指定轴的最小值的索引,忽略 NaN。 -
argwhere(a):返回数组中非 0 元素的索引,按元素分组。 -
nonzero(a):返回数组中非 0 元素的索引。 -
flatnonzero(a):返回数组中非 0 元素的索引,并铺平。 -
where(条件,x,y):根据指定条件,从指定行、列返回元素。 -
searchsorted(a,v ,side,sorter):查找要插入元素以维持顺序的索引。 -
extract(condition,arr):返回满足某些条件的数组的元素。 -
count_nonzero(a):计算数组中非 0 元素的数量。
选取其中的一些方法举例:
a = np.random.randint(0, 10, 20)
a
array([0, 5, 6, 0, 2, 6, 9, 5, 2, 4, 9, 5, 9, 1, 7, 3, 7, 0, 4, 0])
np.argmax(a)
6
np.argmin(a)
0
np.nonzero(a)
(array([ 1, 2, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 18]),)
np.count_nonzero(a)
16
91.9. 总结#
本章节主要是学习了 NumPy 的使用方法和技巧。我们了解了 NumPy 的数值类型和多维数组的概念,然后对 NumPy 数组的操作和抽样方法进行了练习。课程还学习了使用 NumPy 执行代数运算的相关方法,并在最后对 NumPy 索引和切片等方法进行了实战。
学习完本章节,实际上已经基本掌握了 NumPy 使用,但后续还需要通过实战练习来熟悉这些方法。
○ 欢迎分享本文链接到你的社交账号、博客、论坛等。更多的外链会增加搜索引擎对本站收录的权重,从而让更多人看到这些内容。
