10. 逻辑回归实现与应用#
10.1. 介绍#
逻辑回归（Logistic Regression），又叫逻辑斯蒂回归，是机器学习中一种十分基础的分类方法，由于算法简单而高效，在实际场景中得到了广泛的应用。本次实验中，我们将探索逻辑回归的原理及算法实现，并使用 scikit-learn 构建逻辑回归分类预测模型。
10.2. 知识点#
线性可分和不可分
Sigmoid 分布函数
逻辑回归模型
对数损失函数
梯度下降法
逻辑回归，当你听到这个名字之后，我相信你首先注意到的是「回归」。前面我们已经学习了线性回归，那么逻辑回归有何其有什么区别与联系呢。
不过，本次实验刚开始就需要强调：逻辑回归是一种分类方法，而并不是回归方法。你需要牢牢记住，不要混淆。那么，逻辑回归为什么要取一个带「回归」字样的名字呢？它真的和前面所说的回归方法一点关系都没有吗？
关于这个问题，学习完本次实验的全部内容，相信你就会得到答案。
10.3. 线性可分和不可分#
首先，我们需要先接触一个概念，那就是线性可分。如下图所示，二维平面内，如果只使用一条直接就可以将样本分开，则称为线性可分，否则为线性不可分。
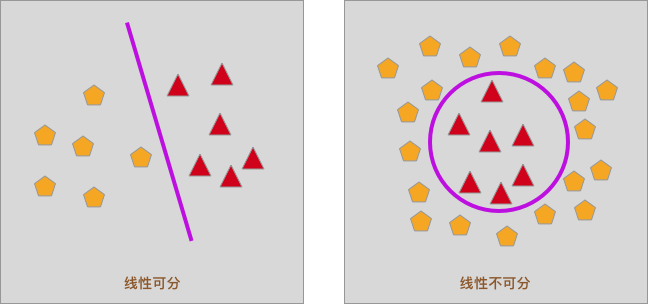
当然，如果在三维空间内，可以通过一个平面去将样本分开，也称为线性可分。由于本次实验不会涉及，这里就先不深入了。
10.4. 使用线性回归分类#
前面的实验中，我们重点学习了线性回归。简单概括起来，线性回归是通过拟合一条直线去预测更多的连续值。其实，除了回归问题，线性回归也可以用来处理特殊情况下的分类问题。例如：
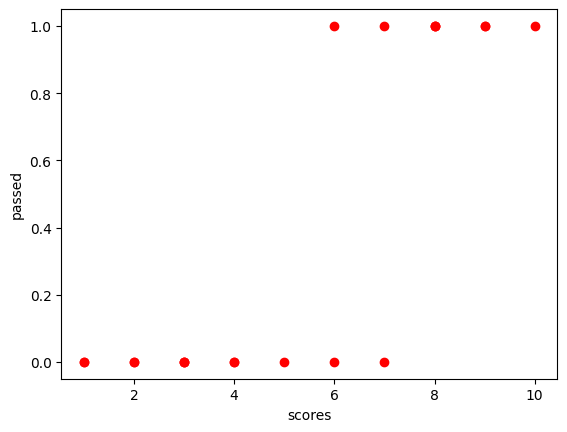
如果我们有如下的数据集，这个数据集仅包含有 1 个特征和 1 个目标值。例如，我们对某一门课程的学员成绩进行统计，通过学习时长决定这门课程是否 PASS。
scores = [
[1],
[1],
[2],
[2],
[3],
[3],
[3],
[4],
[4],
[5],
[6],
[6],
[7],
[7],
[8],
[8],
[8],
[9],
[9],
[10],
]
passed = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1]
上面的数据集中，passed
只有
\(0\) 和
\(1\)，也就是数值型数据。不过，这里我们将
\(0\) 和
\(1\)
分别表示为通过和不通过，那么就转换成了一个分类问题。并且，这是一个典型的二分类问题。二分类表示只有两种类别，也可以称之为：\(0-1\)
分类问题。
对于这样一个二分类问题，怎样用线性回归去解决呢？
在这里，我们可以定义：通过线性拟合函数
\(f(x)\)
计算的结果
\(f(x)>0.5\)
（靠近 1）代表
PASS，而
\(f(x)<=0.5\)
（靠近 0）代表不通过。
这样，就可以巧妙地使用线性回归去解决二分类问题了。
下面，我们就开始实战内容。首先，绘制数据集对应到二维平面中的散点图。
from matplotlib import pyplot as plt
%matplotlib inline
plt.scatter(scores, passed, color="r")
plt.xlabel("scores")
plt.ylabel("passed")
Text(0, 0.5, 'passed')
然后，我们使用 scikit-learn 完成线性回归拟合的过程，相信通过学习前面的内容，你应该对线性回归拟合过程十分熟悉了。
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(scores, passed)
model.coef_, model.intercept_
(array([0.1446863]), -0.36683738796414866)
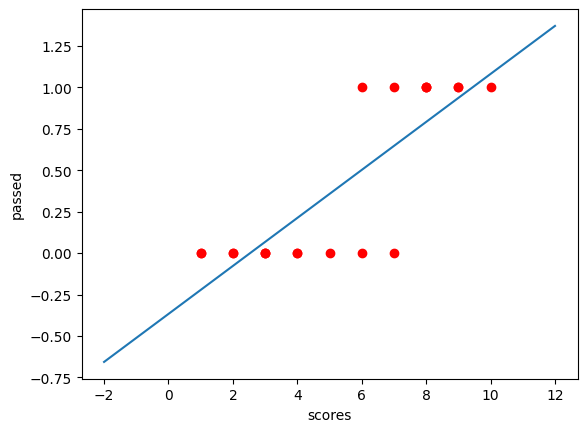
接下来，将拟合直线绘制到散点图中。
import numpy as np
x = np.linspace(-2, 12, 100)
plt.plot(x, model.coef_[0] * x + model.intercept_)
plt.scatter(scores, passed, color="r")
plt.xlabel("scores")
plt.ylabel("passed")
Text(0, 0.5, 'passed')
如果按照上面的定义，即通过线性拟合函数
\(f(x)\)
计算的结果
\(f(x)>0.5\)
代表
PASS，而
\(f(x)<=0.5\)
代表不通过。
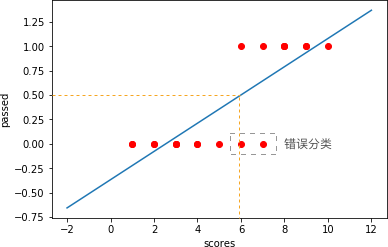
那么，如下图所示，凡是
scores
大于橙色竖线对应
\(x\)
坐标值的部分均会被判断为
PASS，也就是被棕色选框圈出的
2
个点就被错误分类。
10.5. Sigmoid 分布函数#
上面的内容中，虽然我们可以使用线性回归解决二分类问题，但它的结果并不理想。尤其是在完成 \(0-1\) 分类问题中，线性回归在计算过程中还可能产生负值或大于 \(1\) 的数。所以，在今天的实验内容，我们可以通过一种叫做逻辑回归的方式来更好地完成 \(0-1\) 分类问题。
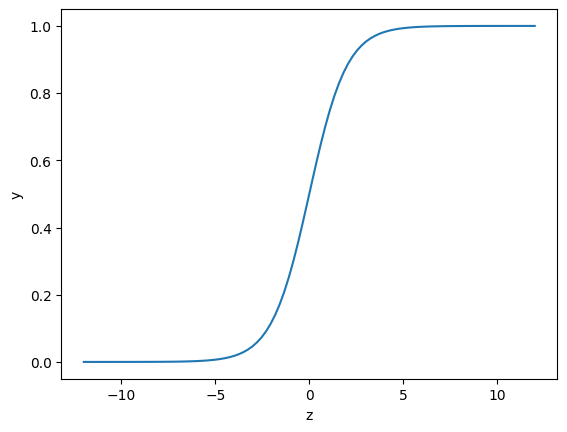
这里, 我们需要先接触到一个叫做 Sigmoid 的函数，这个函数的定义如下：
你可能感觉有一些懵，为什么突然要介绍这样一个函数呢？下面，我们将这个函数的曲线绘制出来看一看，或许你就明白了。
def sigmoid(z):
sigmoid = 1 / (1 + np.exp(-z))
return sigmoid
z = np.linspace(-12, 12, 100) # 生成等间距 x 值方便绘图
plt.plot(z, sigmoid(z))
plt.xlabel("z")
plt.ylabel("y")
Text(0, 0.5, 'y')
上图就是 Sigmoid 函数的图像，你会惊讶地发现，这个图像呈现出完美的 S 型（Sigmoid 的含义）。它的取值仅介于 \(0\) 和 \(1\) 之间，且关于 \(z=0\) 轴中心对称。同时当 \(z\) 越大时，\(y\) 越接近于 \(1\)，而 \(z\) 越小时，\(y\) 越接近于 \(0\)。如果我们以 \(0.5\) 为分界点，将 \(>0.5\) 或 \(<0.5\) 的值分为两类，这不就是解决 \(0-1\) 二分类问题的完美选择嘛。
10.6. 逻辑回归模型#
前面的例子中，实验通过线性回归去完成分类问题。发现拟合后的线性函数的 y 值介于 \(\left ( - \infty,+ \infty \right )\) 之间。其中提到了 Sigmoid 函数，它的 \(y\) 值介于 \(\left ( 0,1 \right )\) 之间。
这里又要引入一条数学定义。那就是，如果一组连续随机变量符合 Sigmoid 函数样本分布，就称作为逻辑分布。逻辑分布是概率论中的定理，是一种连续型的概率分布。
那么，这里就考虑将二者结合起来，也就是把线性函数拟合的结果使用 Sigmoid 函数压缩到 \(\left ( 0,1 \right )\) 之间。如果线性函数的 \(y\) 值越大，也就代表概率越接近于 1，反之接近于 0。
所以，在逻辑回归中，定义：
公式 \((3)\) 中，我们对每一个特征 \(x\) 乘上系数 \(w\)，然后通过 Sigmoid 函数计算 \(f(z)\) 值得到概率。其中，\(z\) 可以被看作是分类边界。故：
由于目标值 \(y\) 只有 0 和 1 两个值，那么如果记 \(y=1\) 的概率为 \(h_{w}(x)\)，则此时 \(y=0\) 的概率为 \(1-h_{w}(x)\)。那么，我们可以记作逻辑回归模型条件概率分布：
上方公式 \((5)\) 不方便计算，其可等价写为似然函数：
你可以验证公式 \((6)\) 的含义为，当 \(y=1\) 是，概率为 \(h_{w}(x)\)，\(y=0\) 的概率为 \(1-h_{w}(x)\)。
上面我们只是拿一个样本举例，对于 \(i\) 个样本的总概率而言实际上可以看作单样本概率的乘积，记为 \(L(w)\)：
由于连乘表示起来非常复杂，我们应用数学技巧，即两边取对数将连乘转换为连加的形式，即：
10.7. 对数损失函数#
实际上，公式 \((8)\) 被称为对数似然函数，该函数衡量了事件发生的总概率。根据最大似然估计原理，只需要通过对 \(L(w)\) 求最大值，即得到 \(w\) 的估计值。而在机器学习问题中，我们需要一个损失函数，并通过求其最小值来进行参数优化。所以，对数似然函数取负数就可以被作为逻辑回归的对数损失函数：
为了衡量整个数据集上的平均损失，所以公式 \((9)\) 在全部样本上求取了平均值，构成逻辑回归最终的对数损失函数。此时，你可能会想到逻辑回归为什么不用线性回归中的平方损失函数呢？
这其实是有数学依据的。我们设置损失函数的目的是接下来通过最优化方法求得损失函数的最小值，损失最小即代表模型最优。在最优化求解中，只有 凸函数 往往才能求得全局最小值，非凸函数往往得到的是局部最优。然而，平方损失函数用于逻辑回归求解时得到的是非凸函数，即大多数情况下无法求得全局最优。这里使用了对数损失函数就避免了这个问题。
如上所示的非凸函数中，存在全局最小值 Global Minimum 和局部最小值 Local Minimum。
当然，上面这句话涉及到很多数学知识。尤其是像最优化理论，是研究生课程阶段才会涉及到的内容，理解起来会有一些困难。如果你无法理解，就记住逻辑回归中，我们使用到的是对数损失函数即可。
下面，我们用代码实现公式 \((9)\) ：
def loss(h, y):
loss = (-y * np.log(h) - (1 - y) * np.log(1 - h)).mean()
return loss
10.8. 梯度下降法#
上面，我们已经成功定义并实现了对数损失函数。所以，现在离求解最优参数只有一步之遥了，那就是求得损失函数的极小值。
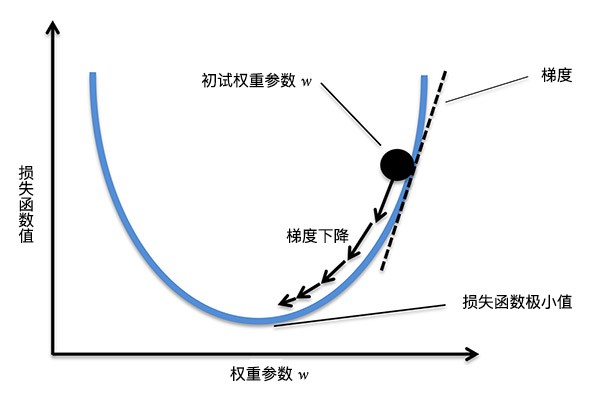
为了求解公式 \((9)\) 的极小值，这里引入一种叫「梯度下降」的求解方法。梯度下降法是一种十分常用且经典的最优化算法，通过这种方法我们就能快速找到函数的最小值。下面将讲解梯度下降法的原理，希望你能认真理解，后面的许多内容都会运用到梯度下降方法。
要理解梯度下降，首先得清楚什么是「梯度」？梯度是一个向量，它表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）。简而言之，对于一元函数而言，梯度就是指在某一点的导数。而对于多元函数而言，梯度就是指在某一点的偏导数组成的向量。
既然，函数在沿梯度方向变化最快，所以「梯度下降法」的核心就是，我们沿着梯度下降方向去寻找损失函数的极小值（梯度的反方向）。过程如下图所示。
所以，我们针对公式 \((9)\) 求偏导数，得到梯度。但现在式 \((9)\) 比较复杂，所以先对式 \((9)\) 进行化简，先来看 \(\log (h_{w}(x^{(i)}))\)，结合式 \((4)\) 得：
同理，来看 \( \log(1-h_{w}(x^{(i)}))\)：
将式 \((10)\) 和式 \((11)\) 带入式 \((9)\) 并化简得：
现在对式 \((12)\) 求导得：
将式 \((4)\) 带入式 \((13)\) 得：
为了便于理解，将式 \((14)\) 用向量的形式表达得：
当我们得到梯度的方向，然后乘以一个常数 \(\alpha\)，就可以得到每次梯度下降的步长(上图箭头的长度)。最后，通过多次迭代，找到梯度变化很小的点，也就对应着损失函数的极小值了。其中，常数 \(\alpha\) 往往也被称之为学习率 Learning Rate。执行权重更新的过程为：
下面，我们用代码实现公式 \((15)\) ：
def gradient(X, h, y):
gradient = np.dot(X.T, (h - y)) / y.shape[0]
return gradient
10.9. 逻辑回归 Python 实现#
实验到目前为止，我们已经具备了实施逻辑回归的基本要素。接下来，就通过一组示例数据，使用逻辑回归完成分类任务。首先，下载并加载示例数据。数据集名称为：course-8-data.csv。
wget -nc https://cdn.aibydoing.com/aibydoing/files/course-8-data.csv
import pandas as pd
df = pd.read_csv("course-8-data.csv", header=0,) # 加载数据集
df.head() # 预览前 5 行数据
| X0 | X1 | Y | |
|---|---|---|---|
| 0 | 5.1 | 3.5 | 0 |
| 1 | 4.9 | 3.0 | 0 |
| 2 | 4.7 | 3.2 | 0 |
| 3 | 4.6 | 3.1 | 0 |
| 4 | 5.0 | 3.6 | 0 |
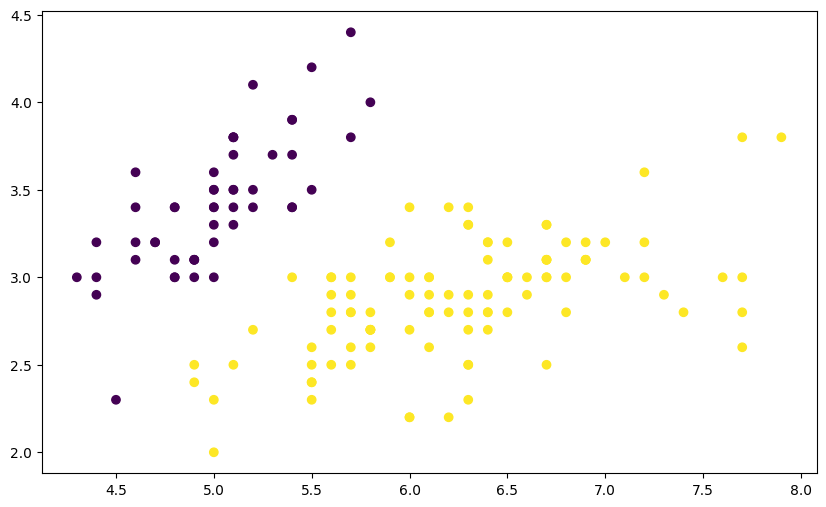
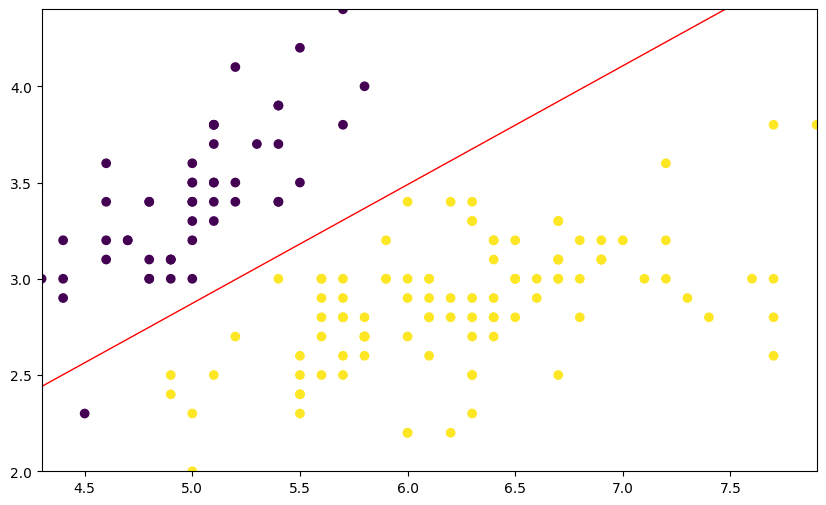
可以看到，该数据集共有两个特征变量 X0 和 X1, 以及一个目标值 Y。其中，目标值 Y 只包含 0 和 1，也就是一个典型的 0-1 分类问题。我们尝试将该数据集绘制成图，看一看数据的分布情况。
plt.figure(figsize=(10, 6))
plt.scatter(df["X0"], df["X1"], c=df["Y"])
<matplotlib.collections.PathCollection at 0x17b830d00>
面对上图中，深蓝色代表 0，黄色代表 1。接下来，就运用逻辑回归完成对 2 类数据划分。也就是公式 \((3)\) 中的线性函数。
为了更方便代码的展示，这里将上面提到的逻辑回归模型、损失函数以及梯度下降的代码集中到一起呈现。接下来，就使用 Python 实现逻辑回归的代码。
def sigmoid(z):
# Sigmoid 分布函数
sigmoid = 1 / (1 + np.exp(-z))
return sigmoid
def loss(h, y):
# 损失函数
loss = (-y * np.log(h) - (1 - y) * np.log(1 - h)).mean()
return loss
def gradient(X, h, y):
# 梯度计算
gradient = np.dot(X.T, (h - y)) / y.shape[0]
return gradient
def Logistic_Regression(x, y, lr, num_iter):
# 逻辑回归过程
intercept = np.ones((x.shape[0], 1)) # 初始化截距为 1
x = np.concatenate((intercept, x), axis=1)
w = np.zeros(x.shape[1]) # 初始化参数为 0
for i in range(num_iter): # 梯度下降迭代
z = np.dot(x, w) # 线性函数
h = sigmoid(z) # sigmoid 函数
g = gradient(x, h, y) # 计算梯度
w -= lr * g # 通过学习率 lr 计算步长并执行梯度下降
l = loss(h, y) # 计算损失函数值
return l, w # 返回迭代后的梯度和参数
然后，我们设定学习率和迭代次数，对数据进行训练。
x = df[["X0", "X1"]].values
y = df["Y"].values
lr = 0.01 # 学习率
num_iter = 30000 # 迭代次数
# 训练
L = Logistic_Regression(x, y, lr, num_iter)
L
(0.05103697443193302, array([-1.47673791, 4.27250311, -6.9234085 ]))
根据我们计算得到的权重，分类边界线的函数为：
\(L[*][*]\) 是从 \(L\) 数组中选择相应取值。
有了分类边界线函数，我们就可以将其绘制到原图中，看一看分类的效果到底如何。下面这段绘图代码涉及到 Matplotlib 绘制轮廓线，不需要掌握。
plt.figure(figsize=(10, 6))
plt.scatter(df["X0"], df["X1"], c=df["Y"])
x1_min, x1_max = (
df["X0"].min(),
df["X0"].max(),
)
x2_min, x2_max = (
df["X1"].min(),
df["X1"].max(),
)
xx1, xx2 = np.meshgrid(np.linspace(x1_min, x1_max), np.linspace(x2_min, x2_max))
grid = np.c_[xx1.ravel(), xx2.ravel()]
probs = (np.dot(grid, np.array([L[1][1:3]]).T) + L[1][0]).reshape(xx1.shape)
plt.contour(xx1, xx2, probs, levels=[0], linewidths=1, colors="red")
<matplotlib.contour.QuadContourSet at 0x17b882770>
可以看出，上图中红线代表我们得到的分割线，也就是线性函数。它比较符合两类数据的分离趋势。
除了绘制决策边界，也就是分割线。我们也可以将损失函数的变化过程绘制处理，看一看梯度下降的执行过程。
def Logistic_Regression_(x, y, lr, num_iter):
intercept = np.ones((x.shape[0], 1)) # 初始化截距为 1
x = np.concatenate((intercept, x), axis=1)
w = np.zeros(x.shape[1]) # 初始化参数为 1
l_list = [] # 保存损失函数值
for i in range(num_iter): # 梯度下降迭代
z = np.dot(x, w) # 线性函数
h = sigmoid(z) # sigmoid 函数
g = gradient(x, h, y) # 计算梯度
w -= lr * g # 通过学习率 lr 计算步长并执行梯度下降
l = loss(h, y) # 计算损失函数值
l_list.append(l)
return l_list
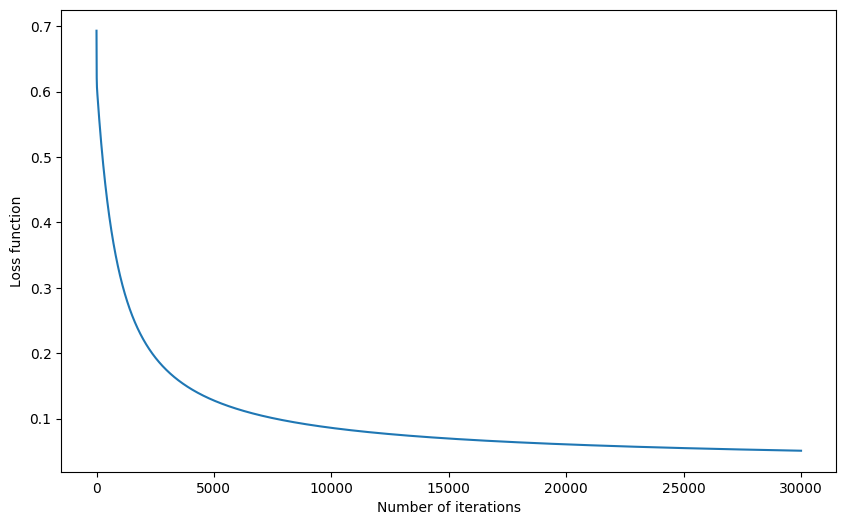
l_y = Logistic_Regression_(x, y, lr, num_iter) # 训练
# 绘图
plt.figure(figsize=(10, 6))
plt.plot([i for i in range(len(l_y))], l_y)
plt.xlabel("Number of iterations")
plt.ylabel("Loss function")
Text(0, 0.5, 'Loss function')
你会发现迭代到 20000 次之后，数据趋于稳定，也就接近于损失函数的极小值。你可以自行更改学习率和迭代次数尝试。
10.10. 逻辑回归 scikit-learn 实现#
上文的内容中，我们了解了逻辑回归的原理以及 Python 实现方式。这个过程很繁琐，但还是很有意义的。我们非常推荐你能至少搞清楚原理部分 80% 的内容。接下来，我们介绍 scikit-learn 中的逻辑回归方法，这个过程就会简单很多。
在 scikit-learn 中，实现逻辑回归的类及默认参数是：
LogisticRegression(penalty='l2', dual=False, tol=0.0001, C=1.0, fit_intercept=True, intercept_scaling=1, class_weight=None, random_state=None, solver='liblinear', max_iter=100, multi_class='ovr', verbose=0, warm_start=False, n_jobs=1)
介绍其中几个常用的参数，其余使用默认即可：
-
penalty: 惩罚项，默认为 \(L_{2}\) 范数。 -
dual: 对偶化，默认为 False。 -
tol: 数据解算精度。 -
fit_intercept: 默认为 True，计算截距项。 -
random_state: 随机数发生器。 -
max_iter: 最大迭代次数，默认为 100。
另外，solver
参数用于指定求解损失函数的方法。默认为
liblinear（0.22 开始默认为
lbfgs），适合于小数据集。除此之外，还有适合多分类问题的
newton-cg,
sag,
saga
和
lbfgs
求解器。这些方法都来自于一些学术论文，有兴趣可以自行搜索了解。
那么，我们使用 scikit-learn 构建逻辑回归分类器的代码如下：
from sklearn.linear_model import LogisticRegression
model = LogisticRegression(
tol=0.001, max_iter=10000, solver="liblinear"
) # 设置数据解算精度和迭代次数
model.fit(x, y)
model.coef_, model.intercept_
(array([[ 2.49579289, -4.01011301]]), array([-0.81713932]))
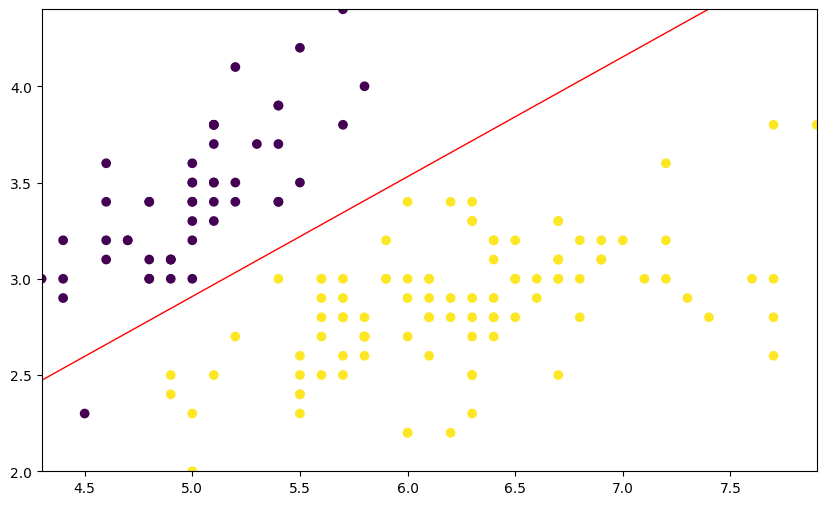
你可能会发现得到的参数和上文 Python 实现得到的参数不一致，原因是我们的求解器不同。同样，我们可以将得到的分类边界线绘制成图。
plt.figure(figsize=(10, 6))
plt.scatter(df["X0"], df["X1"], c=df["Y"])
x1_min, x1_max = df["X0"].min(), df["X0"].max()
x2_min, x2_max = df["X1"].min(), df["X1"].max()
xx1, xx2 = np.meshgrid(np.linspace(x1_min, x1_max), np.linspace(x2_min, x2_max))
grid = np.c_[xx1.ravel(), xx2.ravel()]
probs = (np.dot(grid, model.coef_.T) + model.intercept_).reshape(xx1.shape)
plt.contour(xx1, xx2, probs, levels=[0], linewidths=1, colors="red")
<matplotlib.contour.QuadContourSet at 0x17bcd04f0>
最后，我们可以看一下模型在训练集上的分类准确率：
model.score(x, y)
0.9933333333333333
那么，回到实验一开始的问题，也就是逻辑回归和线性回归之间关系的问题，我相信你应该已经有自己的答案了。
在我看来，「逻辑」二字是对逻辑分布的简称，也代表是与非，0 和 1 之间的逻辑，象征二分类问题。「回归」则源于线性回归，我们通过线性函数构建线性分类边界来达到分类的效果。
10.11. 总结#
本次实验中，我们学习到了一种叫做逻辑回归的分类方法。逻辑回归是非常常见和实用的二分类方法，通常会运用到垃圾邮件判断等实际问题中。另外，逻辑回归其实也可以完成多分类问题，但由于后面要学习在多分类问题上更占优势的其他方法，这里就不再讲解了。
相关链接
○ 欢迎分享本文链接到你的社交账号、博客、论坛等。更多的外链会增加搜索引擎对本站收录的权重，从而让更多人看到这些内容。