85. Q-Learning 强化学习方法实现#
85.1. 介绍#
在强化学习方法中,基于价值的强化学习方法是十分重要的一个分支,本次实验将从案例出发,对基于价值的两个具有代表性的强化学习方法:Q-Learning 和 Sarsa 进行详细介绍,并结合算法流程对 Q-Learning 进行 Python 实现。
85.2. 知识点#
Q-Table 的概念
Q-Learning 算法实现
Sarsa 学习算法
Sarsa 和 Q-Learning 区别
85.3. 强化学习算法分类#
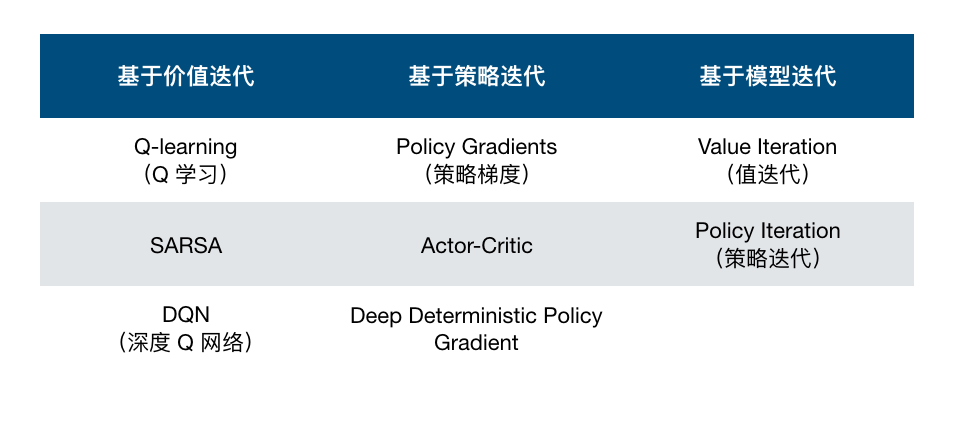
前面,我们给出了如下所示的强化学习算法分类表格。这张表格从基于价值迭代、策略迭代以及模型迭代 3 个维度对强化学习常见算法进行了分类。那么,这 3 个维度是怎样确定的呢?
要回答上面的问题,我们又要回到强化学习过程图示去解释。
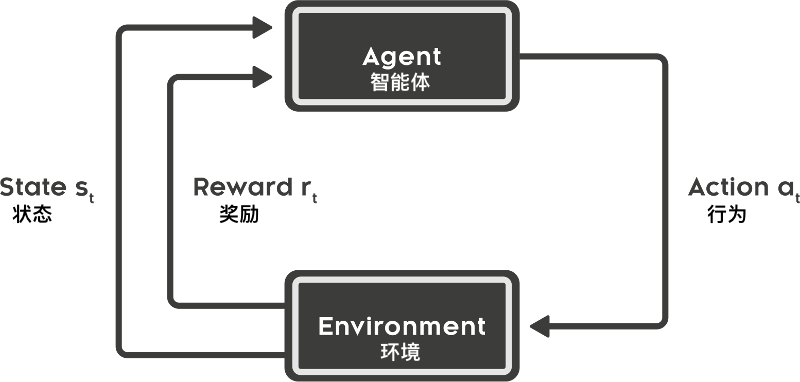
上面这张图呈现了一个典型的强化学习过程,其中的 5 个要素我们都在第一节介绍课程中做了详细的说明。而这一次,我们要重新探寻一下智能体 Agent 的构成。
其实,Agent 的内部通常包含有如下 3 个组件,它们分别是:
-
Policy 策略函数: Agent 的行为,反映 Agent 能采取的行动。其中,状态作为输入,以它的下一步行动决策作为输出。
-
Value function 价值函数: 判断每一次状态(State)或行为(Action)的好坏,类似于评估采取某种行动之后的预期奖励。
-
Model 模型: Model 用于 Agent 感知环境(Environment)的变化。
对于上面的 3 个组件,Agent 并不需要每一次都全部具备,它可以存在一个或多个。而正是依据这 3 个组件,我们得到了强化学习算法分类表格中 3 个分类维度。
所以,更严谨的强化学习算法分类如下:

如上图所示,基于马尔可夫决策过程(MDPs)演化出基于模型和无模型的强化学习方法,而此次强化学习的全部课程集中关注于时间差分学习的部分,并着重于 Q-learning、Sarsa 以及 Policy Gradient 三种最基础的方法。
85.4. 基于价值的强化学习概述#
假定有这样一个游戏场景:小狮子在草原上愉快的玩耍,它知道每一次会有好心人在一个固定的位置放置它最喜欢的大火腿,它希望快速找到大火腿,但是在它到火腿放置点间有许多的陷阱,一碰到陷阱,游戏结束,小狮子只有从头重新寻找合适的路。那么小狮子如何尽快的找到大火腿呢?
最笨的方法:小狮子在尝试中知道并记住陷阱的位置,然后在避开陷阱的情况下,向安全的草坪寻找,直到找到大火腿。显然,想要通过随机寻找出最短路径的方法是不可取的。那除此之外,还有什么好的办法可以解决呢?

首先我们思考一下在现实生活中,遇到不熟悉的环境时,我们会怎么做?
最常规的办法当然是做标记:在经过的草坪上记下前往四个方向(上、下、左、右)探索可能产生的好处 Q(安全或有奖励)。刚开始我们可能会随机的进行移动,并做好标记,当碰到陷阱时,我们会更改标记,给自己做一个提醒。随着标记的增加,我们会根据标记(Q 值)选择下一次的动作,然后根据动作后的结果更新草坪上的 Q 值。
就这样通过反复的自我学习,最终会在整个草坪上做上标记,事实上,更新标记(Q 值)的过程就是熟悉环境的过程,在以后的尝试中通过这些标记就能很快的找到目的地。
将现实生活思考方式应用到我们假定的游戏场景里面会怎么样呢?事实上,其中做标记的 Q 值就是价值(Quality),而根据 Q 值反复的自我学习就是基于价值的强化学习。
85.5. Q-Table 的概念#
上面的案例中,将游戏场景和强化学习五要素结合,很容易一一对应:小狮子即 Agent,草坪即 Environment,每一次移动即 Action,移动到每一个草坪时的状态即 State,移动到相应地方的反馈即 Reward。
将所有草坪上做好的标记 Q 值,组合起来就是一张表,被称之为 Q 值表(Q-Table)。其实,Q-Table 就是基于价值强化学习算法的核心,因为在基于价值的强化学习中,通过 Q-Table 可以决定动作的选择,动作执行后得到的环境反馈 (Reward)目的是更新 Q-Table。
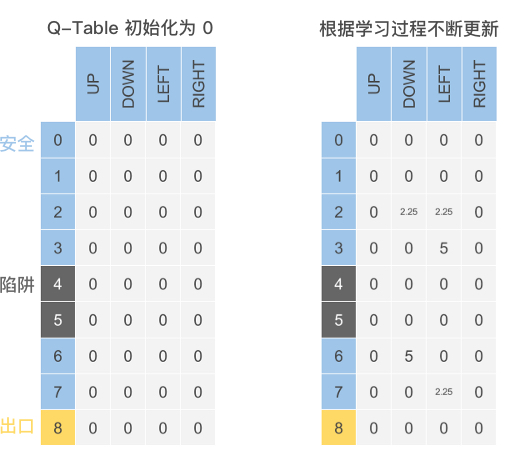
那么,Q-Table 到底长什么样子呢?
如下图所示(其中数据为随机举例),Q-Table 中的列为可选择 Action 动作,每一行数据则由执行不同 Action 对应的 State 状态组成。而存入的数据则为最大期望奖励值(Q 值)。
85.6. Q-Learning 学习算法#
在基于价值的强化学习中,最基本的算法是 Q-Learning 和 Sarsa,其中 Q-Learning 在实际中是应用更加广泛的算法。和案例中小狮子寻找大火腿的方法类似,Q-Learning 算法的原理简述如下:
-
初始化 Q-Table:根据环境及动作种类构建相同维度的表。
行为选择:根据 Q-Table 的值进行动作选择。
行为反馈:采取动作后获取环境所给的行为反馈。
-
Q-Table 更新:根据反馈及未来估计的奖励更新 Q-Table。
然后,重复 2 到 4 步骤,直至达到预想结果或者预先设定迭代次数结束,输出 Q-Table,完成 Q-Learning 学习过程。
根据 Q-Learning 的算法原理,下面我们用 Python 还原小狮子寻找大火腿的游戏场景,并用 Q-Learning 算法来帮助小狮子尽快的找到大火腿。
85.7. Q-Learning 算法实现#
先前就提到过,强化学习的整个流程是在环境中完成的。所以,我们需要搭建一个可以用于算法测试的环境,这也是强化学习的与众不同之处。
我们想要在迷宫中测试使用 Q-Learning 算法来帮助小狮子尽快的找到大火腿。在本地环境中,可以使用 Python 支持的 Tkinter,PyQt 以及 wxPython 来写一个 GUI 的程序,前期过程还是比较复杂的。

本次实验中,为了更直观的理解,同时也为了 Jupyter Notebook
支持,我们将小狮子找火腿的迷宫游戏简化成为一个文字版本。在如下所示的文字游戏中,小狮子用
L
表示,陷阱用
#
表示,大火腿用
$
表示,而普通草坪就用
_
表示。
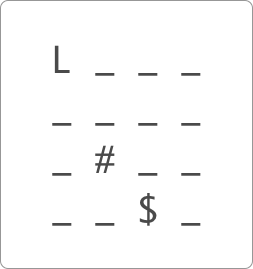
接下来,我们先使用 Python 来完成环境的编写。你无需掌握这部分代码,本次实验重点理解强化学习算法相关的代码即可。
import pandas as pd
import numpy as np
import time
from IPython import display # 引入 display 模块目的方便程序运行展示
def init_env():
start = (0, 0)
terminal = (3, 2)
hole = (2, 1)
env = np.array([["_ "] * 4] * 4) # 建立一个 4*4 的环境
env[terminal] = "$ " # 目的地
env[hole] = "# " # 陷阱
env[start] = "L " # 小狮子
interaction = ""
for i in env:
interaction += "".join(i) + "\n"
print(interaction)
init_env()
L _ _ _
_ _ _ _
_ # _ _
_ _ $ _
可以看到,如示意图所示,文字迷宫游戏的环境已经创建好了。
85.8. 初始化 Q-Table#
根据实际环境,绘制出一张
\(4*4\) 的
Q-Table ,在每一个格子中划分出
up,down,left,right
四个方向的空间,实际上为一个
\(4*4*4\)
的表即 4 行,4 列,高度为
4(四个不同的行动方向)。为了更直观的观察
Q-Table,我们用二维表
\(16*4\)
的方式定义 Q-Table,列名为 Action,每一个 State
用一行来表示。
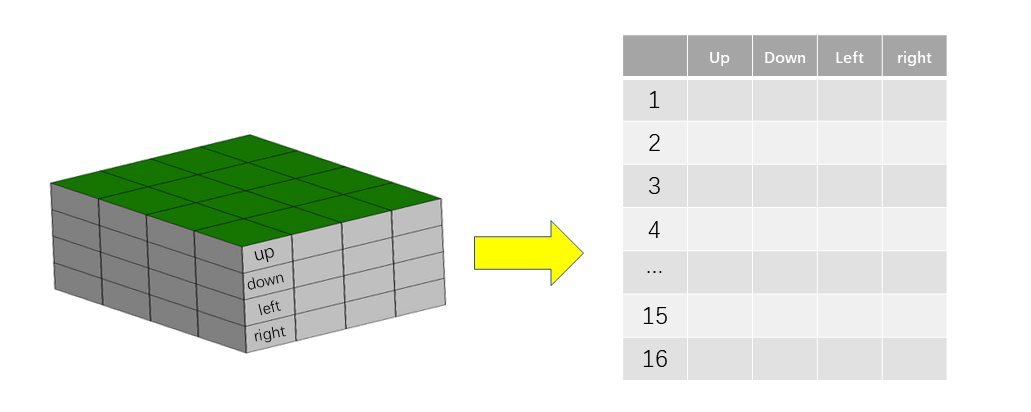
初始化时,我们将 Q-Table 的每一个 Q 值都设置为 0,下面直接使用 Pandas 中的 DataFrame 来输出初始化状态的 Q-Table:
def init_q_table():
# Q-Table 初始化
actions = np.array(["up", "down", "left", "right"])
q_table = pd.DataFrame(
np.zeros((16, len(actions))), columns=actions
) # 初始化 Q-Table 全为 0
return q_table
init_q_table()
| up | down | left | right | |
|---|---|---|---|---|
| 0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3 | 0.0 | 0.0 | 0.0 | 0.0 |
| 4 | 0.0 | 0.0 | 0.0 | 0.0 |
| 5 | 0.0 | 0.0 | 0.0 | 0.0 |
| 6 | 0.0 | 0.0 | 0.0 | 0.0 |
| 7 | 0.0 | 0.0 | 0.0 | 0.0 |
| 8 | 0.0 | 0.0 | 0.0 | 0.0 |
| 9 | 0.0 | 0.0 | 0.0 | 0.0 |
| 10 | 0.0 | 0.0 | 0.0 | 0.0 |
| 11 | 0.0 | 0.0 | 0.0 | 0.0 |
| 12 | 0.0 | 0.0 | 0.0 | 0.0 |
| 13 | 0.0 | 0.0 | 0.0 | 0.0 |
| 14 | 0.0 | 0.0 | 0.0 | 0.0 |
| 15 | 0.0 | 0.0 | 0.0 | 0.0 |
85.9. Action 行为选择#
在得到 Q-Table 之后,如何根据 Q-Table 进行下一步的行为策略呢?
依照常理,肯定是选择最优的决策(Q 值最大的动作),来最大化长期奖励。但这样又会出现一些问题,那就是:在最开始的学习中,由于 Q-Table 中的值为随机的,对于学习没有任何意义,容易出错。在学习一段时间后,由于表值的固定将使得每一次的路线都是固定,不能对环境进行有效探索,容易陷入局部最优问题。
那么应该如何进行行为选择呢?
\(\varepsilon -greedy\) 算法提供了一个较好的解决方案。简单来讲,就是在选择动作的时候,引入一个概率值,在一定概率下按照最优策略进行选择,在一定概率下进行随机选择,这样就可以在尽量选择最优决策的同时,做到对环境的探索。
接下来,就实现行为选择的函数:
def act_choose(state, q_table, epsilon):
"""
参数:
state -- 状态
q_table -- Q-Table
epsilon -- 概率值
返回:
action --下一步动作
"""
state_act = q_table.iloc[state, :]
actions = np.array(["up", "down", "left", "right"])
if np.random.uniform() > epsilon or state_act.all() == 0:
action = np.random.choice(actions)
else:
action = state_act.idxmax()
return action
85.10. 行为反馈 Reward#
Agent 小狮子在每一次动作 Action 执行之后,立即进入下一个 State 时,都会得到环境的反馈 Reward,从而帮助自身学习。
这里,我们设定环境中,终点处的奖励值为 10,陷阱处的奖励值为 -10。同时,为了帮助模型快速收敛,也就是让小狮子尽快的找到最短路径,我们将每走一步的奖励值设为 -1。这也是一个小的技巧,使得 Agent 走更远的路线以及在某个区域打转都会受到惩罚。
接下来,编写 Agent 的反馈函数:
def env_feedback(state, action, hole, terminal):
"""
参数:
state -- 状态
action -- 动作
hole -- 陷阱位置
terminal -- 终点位置
返回:
next_state -- 下一状态
reward -- 奖励
end --结束标签
"""
# 行为反馈
reward = 0.0
end = 0
a, b = state
if action == "up":
a -= 1
if a < 0:
a = 0
next_state = (a, b)
elif action == "down":
a += 1
if a >= 4:
a = 3
next_state = (a, b)
elif action == "left":
b -= 1
if b < 0:
b = 0
next_state = (a, b)
elif action == "right":
b += 1
if b >= 4:
b = 3
next_state = (a, b)
if next_state == terminal:
reward = 10.0
end = 2
elif next_state == hole:
reward = -10.0
end = 1
else:
reward = -1.0
return next_state, reward, end
85.11. Q-Table 更新#
上面已经构建了强化学习的一些基本要素。接下来,就准备让 Agent 开始学习。本次实验中,我们使用到了 Q-Learning 算法,Q-Learning 算法的核心在于 Q-Table 的更新过程。
Q-Learning 采用了 贝尔曼方程(Bellman Equation) 的思想用于 Q-Table 的更新过程,由于贝尔曼方程推导复杂,这里不做详细推导,有兴趣的同学可以通过链接查看。下面我们根据小狮子走迷宫的例子,对 Q-Table 的更新进行详细说明。
假定,小狮子走到右上角格子,定义此时的状态为 \(s_{t}\) ,将移动的方向为 \(a_{t}\),Q-Table 中的当前状态下的采取动作的收益值 Q 则用 \(Q(s_{t},a_{t})\) 表示。定义好基本变量后,接下来直接给出 Q 值更新的公式:

通过上式可以看出 Q 值的更新过程实际上是一个递归迭代的过程。
简单来看 Q 值的更新主要由两部分构成:当前收益值和学习收益值,它们由学习率 \(\alpha\) 连接,当 \(\alpha\) 值越高,说明保留原值效果越少,越看重学习收益值,反之亦然。
当前收益值即 Q-Table 的原值,而学习收益值同样由两部分组成:\(r_{t+1}\) (移动后的奖励)和未来最优值的估计。在这里引用了折损因子,如同一个权重值其作用就是减少当前对后面估计状态的奖励。
由于是递归迭代过程,我们将递归公式展开,以便更深入了解折损因子的作用。为了书写的方便这里我们简写公式。假定 \(Q(s_{1})\) 是初始状态下的收益值,那么 \(Q(s_{1})\) 的更新公式为:
将 \((1)\) 式展开:
其中 \(\gamma\) 为 0 到 1 的数,通过幂计算后可以很容易发现越后面的奖励对于当前估计值影响越小。
接下来,我们实现 Q-Table 更新的函数:
def update_q_table(q_table, state, action, next_state, terminal, gamma, alpha, reward):
"""
参数:
q_table -- Q-Table
state -- 状态
action -- 动作
next_state -- 下一状态
terminal -- 终点位置
gamma -- 折损因子
alpha -- 学习率
reward -- 奖励
返回:
q_table -- 更新后的Q-Table
"""
# Q-Table 的更新函数
x, y = state
next_x, next_y = next_state
q_original = q_table.loc[x * 4 + y, action]
if next_state != terminal:
q_predict = reward + gamma * q_table.iloc[next_x * 4 + next_y].max()
else:
q_predict = reward
q_table.loc[x * 4 + y, action] = (1 - alpha) * q_original + alpha * q_predict
return q_table
为了便于观察小狮子一步一步训练找到大火腿的过程,下面我们定义一个辅助函数。该函数方便于展示小狮子每一步状态的可视化函数。
def show_state(end, state, episode, step, q_table):
"""
参数:
end -- 结束标签
state -- 状态
episode -- 迭代次数
step --迭代步数
q_table-- Q-Table
"""
# 状态可视化辅助函数
terminal = (3, 2)
hole = (2, 1)
env = np.array([["_ "] * 4] * 4)
env[terminal] = "$ "
env[hole] = "# "
env[state] = "L "
interaction = ""
for i in env:
interaction += "".join(i) + "\n"
if state == terminal:
message = "EPISODE: {}, STEP: {}".format(episode, step)
interaction += message
display.clear_output(wait=True) # 清除输出内容
print(interaction)
print("\n" + "q_table:")
print(q_table)
time.sleep(3) # 在成功到终点时,等待 3 秒
else:
display.clear_output(wait=True)
print(interaction)
print(q_table)
time.sleep(0.3) # 在这里控制每走一步所需要时间
定义好可视化函数之后,接下来按照 Q-Learning 算法流程对 Q-Learning 进行实现。这里给出 Q-Learning 算法的伪代码和解释如下:
Initialize Q arbitrarily // 随机初始化 Q 值
Repeat (for each episode): // 每一次游戏称之为一个 episode
Initialize S // 小狮子初始位置的状态
Repeat (for each step of episode):
根据当前 Q 和位置 S,使用 ε-greedy 策略,得到动作 A
做了动作A,小狮子到达新的位置S',并获得奖励 R
Q(S,A) ← (1-α)*Q(S,A) + α*[R + γ*maxQ(S',a)] // 在 Q 中更新 S
S ← S'
until S is terminal // 小狮子找到大火腿或者掉到陷阱即重新开始
伪代码中 Q-Table 的更新公式同 3.5 中所讲的 Q-Table 的更新公式只是表现形式的差异,实际意义相同。
下面,给出 Q-Learning 算法的完整实现函数:
def q_learning(max_episodes, alpha, gamma, epsilon):
"""
参数:
max_episodes -- 最大迭代次数
alpha -- 学习率
gamma -- 折损因子
epsilon -- 概率值
返回:
q_table -- 更新后的Q-Table
"""
q_table = init_q_table()
terminal = (3, 2)
hole = (2, 1)
episodes = 0
while episodes <= max_episodes:
step = 0
state = (0, 0)
end = 0
show_state(end, state, episodes, step, q_table)
while end == 0:
x, y = state
act = act_choose(x * 4 + y, q_table, epsilon) # 动作选择
next_state, reward, end = env_feedback(state, act, hole, terminal) # 环境反馈
q_table = update_q_table(
q_table, state, act, next_state, terminal, gamma, alpha, reward
) # q-table 更新
state = next_state
step += 1
show_state(end, state, episodes, step, q_table)
if end == 2:
episodes += 1
现在终于将 Q-Learning 整个算法实现,可以帮助小狮子找到大火腿了。接下来,我们指定参数,并执行函数来观测小狮子是如何利用 Q-Learning 算法找到前往大火腿放置点的最短路径。
q_learning(max_episodes=10, alpha=0.8, gamma=0.9, epsilon=0.9)
_ _ _ _
_ _ _ _
_ # _ _
_ _ L _
EPISODE: 10, STEP: 5
q_table:
up down left right
0 -2.382398 3.094751 -2.213120 -2.284452
1 -2.213120 -2.134708 -2.238334 -1.804800
2 -1.536000 -1.568000 -2.230358 -1.651200
3 -1.536000 -0.998400 -1.683200 -1.536000
4 -0.302803 4.575375 -1.536000 -1.536000
5 -1.719450 -9.600000 -0.195464 -1.691187
6 -1.376000 -0.999680 -1.897574 -1.689600
7 -1.852160 -1.536000 -1.710848 -0.992000
8 0.695038 6.199484 -0.992000 -8.000000
9 0.000000 0.000000 0.000000 0.000000
10 -1.876736 0.000000 -8.000000 -0.992000
11 -1.536000 4.800000 -0.960000 -0.800000
12 0.630620 4.650713 -1.536000 7.999966
13 -8.000000 4.800000 3.297792 9.999999
14 0.000000 0.000000 0.000000 0.000000
15 2.656000 4.960000 8.000000 4.960000
通过运行程序可以十分直观的看到,随着迭代的增加,小狮子走的路越来越正确,所用的 STEP 也会越来越少,直到找到最短路径。但在找到最短路径后,仍然可能出现 STEP 增加的情况,这就是因为引入 \(\varepsilon -greedy\) 随机进行探索的结果,是十分正常的现象。
85.12. Sarsa 学习算法#
在基于价值的强化学习算法中,还有一种同 Q-Learning 类似的算法被称之为 Sarsa。下面我们从原理以及算法流程上来简单看一下 Sarsa 学习算法同 Q-Learning 学习算法的不同。
Sarsa 从本质上和 Q-Learning 类似,其中最大的区别就在于 Q-Table 表的更新,下面我们先从伪代码上对 Sarsa 进行了解。

从伪代码中,可以将 Sarsa 的算法流程总结为如下几个步骤 。
-
初始化 Q-Table:根据环境及动作种类构建相同维度的表。(同 Q-Learning)
-
行为选择:根据 Q-Table 的值进行下一步动作选择。(同 Q-Learning)
-
行为反馈:采取动作后获取环境所给的行为反馈。(同 Q-Learning)
-
Q-Table 更新:根据反馈及下一状态实际奖励更新 Q-Table。(区别于 Q-Learning)
重复 2 到 4 步骤,直至达到预想结果或者预先设定迭代次数结束,输出 Q-Table,完成 Sarsa。
你会发现,对比于 Q-Learning 算法的学习流程,Sarsa 只有其中一个步骤描述有所区别。那就是在 Q-Learning 中,我们是根据反馈及未来估计的奖励更新 Q-Table。而 Sarsa 则是根据反馈及下一状态实际奖励更新 Q-Table。
85.13. Sarsa 和 Q-Learning 区别#
关于 Sarsa 和 Q-Learning 算法的区别,不论从伪代码还是算法原理方面,都不能直观的了解,下面我们以一张图的方式来形象的说明。
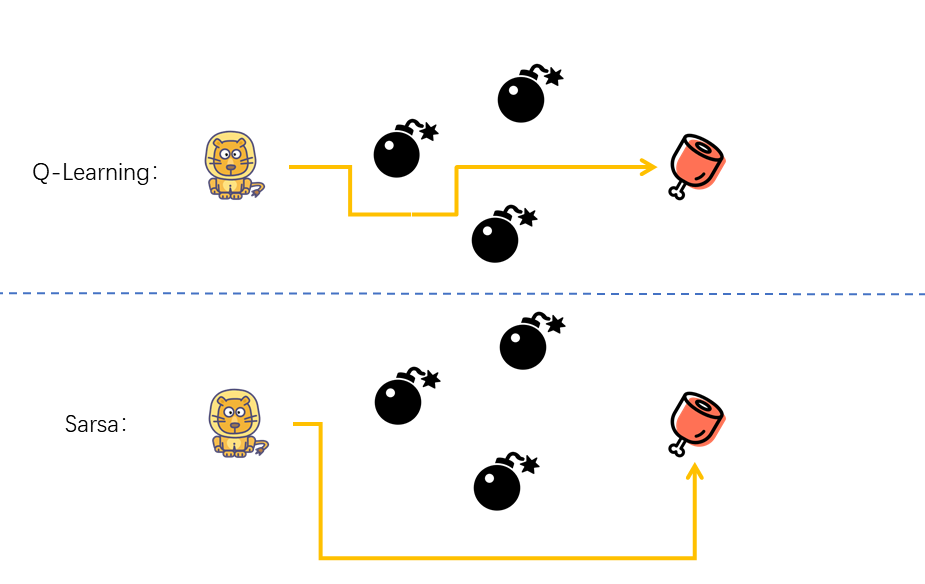
Q-Learning 算法实际上是一种 Off-Policy 的算法,即可以通过估计或者其他的预测来进行学习。
在更新 Q-Table 时,Q-Learning 采用的是「贪婪式」算法,即根据估计得到的未来奖励值的大小进行更新。实际上表现为:小狮子十分具有冒险精神,在选择路径时,将找到大火腿放在第一位,不论路途多么危险,只要能更接近大火腿便往前行动。
相比于 Q-Learning 的通过估计更新 Q-Table 的「理想派」算法,Sarsa 就更加的「务实」,它是一种 On-Policy 的算法,即通过自身经历产生的经验来进行学习。而 On-Policy 表示沿用既定策略,它和 Off-Policy 的 Q-Learning 算法区别如下,即更新 Q 所使用的方法是沿用既定的策略(on-policy)还是使用新策略(off-policy)。
区别 |
Q-Learning |
Sarsa |
|---|---|---|
选择下一步行动 A’ |
ε-greedy policy |
ε-greedy policy |
更新 Q 值 |
greedy policy |
ε-greedy policy |
在更新 Q-Table 时,Sarsa 采用实际行动来进行更新,即进入 \(S_{t+1}\) 后,对 \(Q(S_{t},a)\) 进行更新。实际上表现为:小狮子显得十分谨慎,在选择路径时,更重视陷阱的存在,为了避开陷阱绕路行动。
在完成本次实验的挑战后,通过展示对比,便会发现,采用 Q-Learning 算法比 Sarsa 算法更容易找到合适路径,但是在找到合适路径过程中,Q-Learning 算法比 Sarsa 算法失败的次数要多。
本次实验中,我们就不对 Sarsa 算法进行实现了,你将会在接下来的挑战中,自己动手尝试实现 Sarsa 算法的更新过程。
85.14. 总结#
本次实验对基于价值的强化学习算法进行了详细的介绍,但由于强化学习内容十分抽象,需要大家反复的学习以及训练。
相关链接
○ 欢迎分享本文链接到你的社交账号、博客、论坛等。更多的外链会增加搜索引擎对本站收录的权重,从而让更多人看到这些内容。
