89. Python 概率论和统计学基础#
89.1. 介绍#
概率论是一种用于表示不确定性声明的数学框架。很多机器学习算法的设计都会依赖于对数据的概率假设。同样,我们还可以使用概率和统计的相关知识,从理论上分析我们提出的 AI 系统的行为。 本实验主要是对机器学习中常用的概率论和统计学习方法进行讲述。
89.2. 知识点#
概率公式
随机变量
概率分布
数学期望
方差、标准差和协方差
假设检验
概率论是一种用于表示不确定性声明的数学框架。很多机器学习算法的设计都会依赖于对数据的概率假设。同样我们还可以使用概率和统计的相关知识,从理论上分析我们提出的 AI 系统的行为。接下来,让我们介绍一下概率论中最为重要的几个概率公式。
89.3. 条件概率#
条件概率即在某个条件之下的概率。如当事件 \(A\) 发生时,事件 \(B\) 发生的概率就可以被称作条件概率,记作 \(P(B|A)\)。又比如,给定条件 \(x = a\) 时,\(y=b\) 的概率就是条件概率,记作 \(P(y=b|x=a)\)。括号中竖线右边记录着条件,左边记录着结果。
条件概率 \(P(B|A)\) 的计算公式如下:
举个例子,一个盒子里混有 100 只新旧乒乓球,且这些乒乓球中有红色和黄色两种。分类如下:
黄色 |
白色 |
|
|---|---|---|
新 |
40 |
30 |
旧 |
20 |
10 |
如果我从盒子中取出了一个球,已知该球为 黄色,那么请问该球为新球的概率是多少呢?
我们可以从上表看出,这个黄色球为新球的概率为\( P=\frac{40}{60}\)(因为已经知道是黄色了,所以分母为 60)。
当然,我们也可以使用上面讲到的条件概率的方法:
设事件 A ={从盒子中随机取一个球,该球为黄球},则根据上表可得 \(P(A) =\frac{20+40}{100}=\frac{60}{100}\)。
设事件 B ={从盒子中随机取一个球,该球是新球},则根据上表可知,取出的球为黄色新球的概率为:\(P(AB)=\frac{40}{100}\)。
则取出一个球为黄色球,那么该球也为新球的概率如下:
请注意,这里的事件 \(P(AB)\neq P(A)\times P(B)\),因为事件 A 和事件 B 不独立。
89.4. 全概率公式#
定义:设 \(A_1,A_2,...A_n\),为一列互不相容的事件且 \(A_1 \cup A_2 \cup,... \cup A_n=\Omega\),则对任意事件 B,都存在如下关系:
全概率公式可以通过下图进行解释:
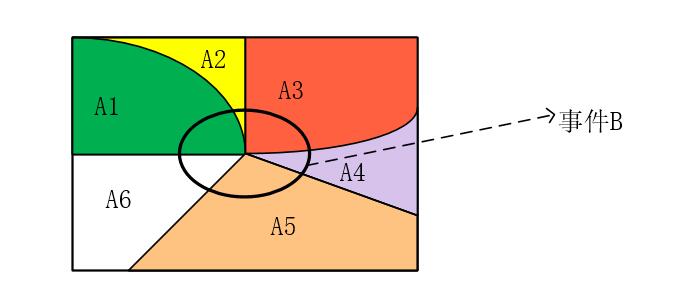
当我们直接求取 \(P(B)\) 非常困难时,我们可以将事件 \(B\) 分成多个部分: $\( P(B) = P(A_1B)+ P(A_2B)+P(A_3B)+P(A_4B)+P(A_5B)\)$
然后再根据条件概率公式,将上列式子转换一下:
这就是全概率公式的来历。该公式的主要思想就是,在计算 \(P(A)\) 较困难时,我们可以通过将事件 \(A\) 分解成几个小事件,通过计算小事件的概率,然后相加,进而求得大事件的概率。
举一个简单的例子,假设某车间使用甲、乙、丙、丁四台机床。各个机床的次品率分别为 5%,4%,3%,3.5%,且它们各自的产品占了总产量的 20%,35%,25%,20%。现在把它们混在一起,问随机取出一个产品为次品的概率。
思路:根据题目描述,我们可以知道:
-
某个产品来自于某个机床的概率 \(P(A_i)=[20\%,35\%,25\%,20\%]\) (使用占比估算概率)。
-
次品率 \(P(B|A_i)=[5\%,4\%,3\%,3.5\%]\)(该次品率为每个机床下的次品率,分母为机床各自的产品数量)。
而我们现在需要求的是 \(P(B)\),即分母为总产品数量的次品率。根据全概率公式,我们可以利用向量乘法求得该产品的中次品率:
import numpy as np
# 将百分数转为小数
pa = np.array([20.0, 35, 25, 20])*0.01
pb_A = np.array([5.0, 4, 3, 3.5])*0.01
# 利用全概率公式计算次品率:先相乘再求和
pb = np.sum(np.multiply(pa, pb_A))
print("总次品率为:{}%".format(pb*100))
总次品率为:3.85%
89.5. 贝叶斯公式#
定义:设 \(A_1,A_2,...A_n\),为一列互不相容的事件且 \(A_1 \cup A_2 \cup,... \cup A_n=\Omega\)。若现在事件 B 已发生, \(A_i\) 发生的概率:
上式即为贝叶斯公式的推导,其实无论是全概率公式的推导还是贝叶斯公式的推导,他们的核心都是使用条件概率公式。
贝叶斯公式和全概率公式的不同:假设这里存在几种方式来达到一个相同的目标,每种方式达到目标的概率不同。全概率公式就是用于计算最终能够达到该目标的概率值(即不管使用哪种方式)。而贝叶斯公式计算的是,已知目标已经达成的条件下,使用每种方式的概率。
还是拿上面机床加工产品举例,设抽出产品为次品为事件 B,第 \(i\) 个机床产生产品为事件 \(A_i\),其他数据不变。
假设现在还是将所有的产品混在一起,然后从中抽出一个产品。发现这个产品是次品,问该产品来自各个机床的概率 \(P(A_i|B)\)。
根据题目,我们需要求的就是 \(P(A_i|B)\) 。那么利用贝叶斯公式,我们可以计算:
# 根据贝叶斯公式,计算来自每个机床的概率
# 这里的 pb 可以通过全概率公式进行计算
pA_b = (pa*pb_A) / pb
for i in range(4):
print("该产品来自第 {} 个机床的概率:{}".format(i+1, pA_b[i]))
该产品来自第 1 个机床的概率:0.25974025974025977
该产品来自第 2 个机床的概率:0.3636363636363637
该产品来自第 3 个机床的概率:0.1948051948051948
该产品来自第 4 个机床的概率:0.18181818181818185
89.6. 概率分布#
89.7. 数据的类型#
在编程中,我们常常需要一些随机值(比如在模拟抛硬币时)。我们将这些存储随机值的变量称之为随机变量。
随机变量根据产生的数值范围不同,可以分成两种类型:
-
离散型随机变量:如果随机变量 \(X\) 只能取有限个或至多个可列值,则称 \(X\) 为离散型随机变量。比如,取集合 \(\{0,1\}\) 的随机变量就为离散型变量(只存在两个值)。
-
连续型随机变量:如果随机变量 \(X\) 的所有可能取值不可以逐个列举出来,而是取数轴上某一区间内的任一点的随机值,则 \(X\) 为连续型随机变量。比如取值为 \((0,1]\) 的随机变量就为连续型变量(0 到 1 之间存在无数个点)。
无论是哪种随机变量,它的产生原理就是给它的范围中的每个可取值赋予一个概率,然后根据概率随机给变量赋值。
描述所有可取值的概率函数又可以根据变量类型不同分为:
-
概率质量函数:描述离散变量的可取值的概率函数。
概率密度函数:描述连续型变量的概率分布函数。
概率分布是指随机变量的概率规律。简单的说,概率分布描述了随机变量的每个可取值,所对应的概率。在模拟数据时,我们根据概率的不同,对数据的取值也不同。接下来,让我们来详细介绍一下常见的离散型概率分布和连续型概率分布函数。
注意,对于初学者,我们不必背下每个函数的具体形式。我们更应该了解的是每种分布函数的特点和适用范围。
89.8. 离散型概率分布#
在生活中,有许多事件的结果往往只有两个。例如:抛硬币的结果(正面朝上或者朝下)、检查产品的质量(合格或不合格)、购买彩票(中奖或不中奖),以上这些事件都可以叫做伯努利实验。
伯努利试验其实就是单次随机试验,且结果只有 0 或 1 两种,由科学家伯努利提出。伯努利实验产生的数据分布就是两点分布。
二点分布:也就是我们最常见的 0-1 分布。服从该分布的变量只有 0 和 1 两种取值。该分布的概率质量函数如下:
其中 \(x\) 的可取值为 \(\{0,1\}\)。\(\lambda\)为结果成功的概率,可以为 \([0,1]\) 中的任意值 。\(P(x)\) 表示结果为 \(x\) 的概率。
我们可以通过每个 \(x\) 所对应的概率来产生随机数。如下:
def Bernoulli(lambd_a):
p = np.random.rand()
# 表示返回 1 的概率 为 lambda
if(p < lambd_a):
return 1
else:
return 0
我们可以利用上面函数进行抛硬币的模拟,假设抛 5 次硬币:
for i in range(5):
print("第{}次实验结果:".format(i+1))
result = Bernoulli(0.5) # 每面的结果概率相同
if(result == 1):
print("正面")
else:
print("反面")
第1次实验结果:
正面
第2次实验结果:
反面
第3次实验结果:
正面
第4次实验结果:
反面
第5次实验结果:
反面
二项分布:进行 \(n\) 次伯努利实验后,结果为 1 的次数的概率分布,即实验成功的次数的概率分布,其中每次试验成功的概率为 \(p\)。
如果一个实验每次成功的概率为 \(p\),然后我们进行了 \(n\) 次试验,问一共成功 \(x\) 次的概率。我们可以通过排列组合得到下面的公式:
其中 \(C_n^x\) 是排列组合,表示从 \(n\) 次试验中选出 \(x\) 次实验。\(p^x\) 表示选出的实验都成功的概率。\((1-p)^{n-x}\) 表示未选出的实验都失败的概率。
其实上面的这个函数就是二项分布的概率质量函数。表示在进行 \(n\) 次概率为 \(p\) 的伯努利实验后,成功 \(x\) 的概率值。其中 \(x\) 是变量,\(n\) 和 \(p\) 是常数。如果随机变量 \(X\) 服从参数为 \(n\) 和 \(p\) 的二项分布,我们可以记为 \(X \sim B(n, p)\)。
注意,通过两点分布返回的是一次抛一个硬币的实验结果(0 或 1)。通过二项分布返回的是每次实验抛 \(n\) 个硬币,且硬币朝上的个数,结果可为 0,1,2,3……
当 \(n=1\) 时,二项分布就是二点分布。
虽然上面的式子较为复杂,但是不需要手动编写。我们可以使用
numpy.random.RandomState.binomial(n,
p,
size=None)
随机初始化 x 的值。
该函数就是利用上面式子所提供的概率值,来随机初始化 \(x\) 的。
n, p = 1000, 0.5
# 每得到一个随机数,都需要抛 1000 个硬币,然后返回其中成功的次数
# 一共得到 10000 个随机数
results = np.random.binomial(n, p, 10000)
results
array([512, 508, 495, ..., 500, 485, 471])
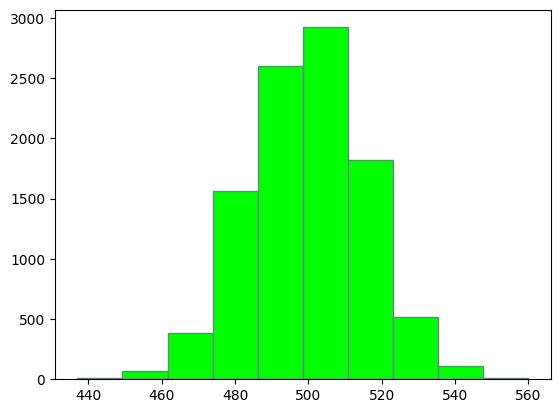
如上,我们进行了 10000 次试验,每次试验抛了 1000 个硬币,并且返回了其中为正面的硬币个数。我们可以将这些个数进行统计,返回每种数值出现的次数,并且画出成功个数的直方图:
import matplotlib.pyplot as plt
%matplotlib inline
plt.hist(results, edgecolor='slategray', facecolor='lime')
从上面可知,进行了多次试验,硬币正面个数为 500 左右的次数最多。这也是非常符合常理的,因为我们每次试验都会抛 1000 个硬币,然后由于硬币正面朝上的概率为 50%。因此,大多数试验的正面朝上次数都在 \(1000\times 50\% = 500\) 左右。
89.9. 连续型概率分布#
离散型概率分布的概率函数叫做概率质量函数。通过上面的学习,我们可以知道,概率质量函数描述的就是概率和可取值 \(x\) 之间的关系。因此,如果我们将所有 x 的概率取值相加就应该等于 1。
但是由于连续型变量的可取值往往不是离散的点,而是一个区间,其中存在着无数个点。因此,在针对连续型概率分布时,我们没有某点概率值的概念(如果有这个概念,无论该点值有多小,乘以一个无穷大,最终的值都远远大于 1)。
我们选择了概率密度函数来表示概率分布。
概率密度函数表示的其实是 概率在该点的变化率。
我们可以把概率和概率密度的关系,看做距离和速度的关系(概率即距离,概率密度即速度)。
就可以得到以下几个结论:
-
说某一个点的距离是没有意义的,因为距离是 XX 到 XX 的概念。
某点速度的概念和某点距离的概念完全不一致
-
因此,在描述连续型概率时,某点的概率是无意义的,只有加上区间才是有意义的。
-
某个区间的总概率值就是概率密度函数在该区间内的面积,可以用定积分表示。
让我们来举几个常见的连续性分布函数的例子。
均匀分布: 产生任何数的概率相等的分布。
均匀分布是我们最常用的分布。该分布的密度函数需要两个参数 a,b。其中 a 表示随机数可取范围的下界,b 表示范围的上界。
该分布的概率密度函数如下:
上面公式就为均匀分布的概率密度公式,即概率的变化率函数。
我们可以通过上列公式和定积分,求得 \((-∞,x)\) 区间的总概率值,如下:
上面的这种,求某区间概率值的函数被称作该连续变量 x 的分布函数。
我们可以使用
np.random.uniform(a,b)
产生服从均匀分布的数据:
# 产生了 10000 条数据
datas = np.random.uniform(10, 20, 10000)
datas
array([11.35253202, 18.10761871, 10.41783694, ..., 13.27334503,
15.87429389, 11.32816989])
让我们来展示一下这些数据的分布情况:
# density=True 表示计算每个区间出现的次数后,除以一下总次数,使横坐标成为占比
plt.hist(datas, density=True, edgecolor='slategray', facecolor='lime')
(array([0.10361532, 0.09621423, 0.09561414, 0.09911466, 0.10241515,
0.1041154 , 0.10171504, 0.09741441, 0.09851457, 0.101415 ]),
array([10.00044859, 11.0003007 , 12.00015281, 13.00000492, 13.99985703,
14.99970914, 15.99956125, 16.99941336, 17.99926548, 18.99911759,
19.9989697 ]),
<BarContainer object of 10 artists>)
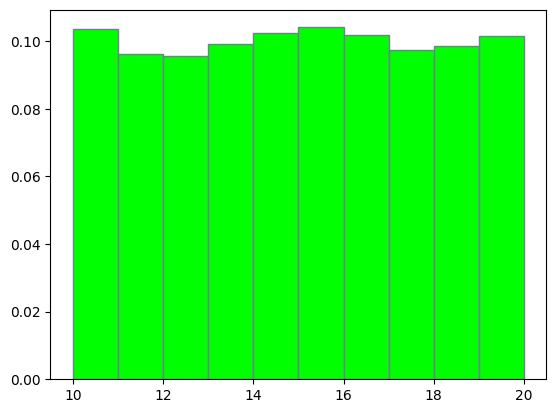
从上图可以看出,产生 0-20 中任意一点的概率都相等。
指数分布:表示一个随机变量呈指数分布,可以写作 \(x \sim E(\lambda)\)。
该分布的概率密度函数如下:
上面公式就为指数分布的概率密度公式,即概率的变化率函数。
我们可以通过概率密度函数和定积分知识,求得指数分布函数如下:
其中 \(F(x)\) 表示范围为 \((-∞,x)\) 的总概率值,\(\lambda\) 为指数分布所需的一个参数。
我们可以利用
np.random.exponential(lambda,size)
来初始化 10000
条服从指数分布的数据,并且根据数据观察指数分布的图像:
datas = np.random.exponential(3, 10000)
datas
array([4.03047872, 4.7548291 , 0.34659548, ..., 5.23667938, 2.82619846,
0.32841398])
让我们统计每个数据出现的次数,画出指数分布的图像。如下:
plt.hist(datas, density=True, edgecolor='slategray', facecolor='lime')
(array([2.24472872e-01, 8.91083550e-02, 3.75949512e-02, 1.59986563e-02,
6.20278872e-03, 2.98792871e-03, 1.09683459e-03, 5.29506354e-04,
1.51287530e-04, 7.56437649e-05]),
array([4.35887905e-04, 2.64440794e+00, 5.28837998e+00, 7.93235203e+00,
1.05763241e+01, 1.32202961e+01, 1.58642682e+01, 1.85082402e+01,
2.11522123e+01, 2.37961843e+01, 2.64401564e+01]),
<BarContainer object of 10 artists>)
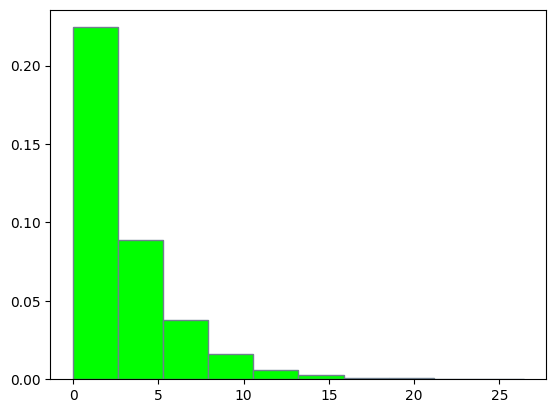
正态分布:
正态分布又叫高斯分布。若随机变量 X 服从正态分布,可以写作 \(x\sim N(\mu,\sigma^2)\)。其中 \(\mu\) 和 \(\sigma\) 是该分布的两个参数。这两个参数其实就是该分布的平均值和标准差。
该分布的概率密度函数如下所示:
我们可以使用
np.random.normal(mu,
sigma,
size)
初始化服从正态分布的随机数:
mu, sigma = 0, 0.1 # 定义分布数据的平均值和标准差
s = np.random.normal(mu, sigma, 1000)
s
array([-1.03212013e-01, 1.34225459e-02, -8.51825733e-02, 1.39488356e-02,
-1.54223413e-01, -6.78743103e-02, -1.09066754e-01, 2.95078420e-03,
9.14926523e-02, 2.18311105e-02, 1.13268319e-01, 8.46439417e-02,
-6.59709435e-02, 1.06736560e-02, 4.74476780e-02, -1.06676872e-01,
5.72988789e-02, -4.54837692e-02, 5.59849027e-02, 1.12364086e-01,
-1.10276381e-01, 7.51001710e-02, 2.14264673e-02, 1.15503133e-01,
-8.56336100e-02, 1.31847207e-02, 1.54110124e-02, -2.58373868e-02,
8.21562165e-02, -1.15138088e-01, 5.62701126e-02, 5.46837310e-02,
7.78349911e-02, 1.32299939e-01, -7.37705083e-02, 8.71036210e-03,
3.78679025e-03, 1.30365076e-02, -1.05973838e-01, -6.61335633e-02,
-8.30134075e-02, 5.63107937e-02, 6.32973591e-02, -1.02907427e-01,
-2.90186222e-02, 9.74900170e-02, -7.45204617e-02, -5.98677335e-02,
1.85138553e-01, 4.55942171e-02, -5.17539703e-02, 2.58750419e-02,
1.19750552e-01, 3.53238246e-02, -9.94301457e-02, 1.98513157e-01,
-1.46224897e-01, 1.02378592e-01, 9.66797044e-02, 4.66401914e-02,
3.54530458e-01, 9.69629220e-03, -3.79025300e-02, 6.57972492e-03,
-1.74890632e-02, -1.35786327e-01, -5.54657391e-02, 5.65163964e-03,
8.24665809e-02, -6.34523217e-03, -1.10999396e-02, -1.42414024e-01,
-4.52386148e-02, -9.41074534e-02, -2.69334875e-01, -1.94842922e-02,
-4.73237383e-02, 9.00397707e-02, 3.87999019e-03, 6.15473307e-02,
8.11657744e-02, 5.52926349e-03, 2.00420205e-01, 2.77779831e-02,
1.04155183e-01, 2.29098340e-01, 3.02839289e-03, -7.62428348e-02,
1.71700692e-01, 2.79456378e-02, -5.57938763e-02, 8.68910720e-02,
-1.76634530e-01, 1.27783514e-02, 6.57111847e-02, -2.01619261e-02,
-1.33760586e-02, -2.96501764e-03, 1.15072227e-01, 1.40382815e-01,
-7.30203980e-02, -2.82478210e-02, -4.28573831e-02, 4.86540059e-02,
5.75251702e-02, -3.58291844e-02, 6.38200990e-02, 9.81212576e-02,
1.62039099e-02, -4.65965099e-02, -4.82808791e-02, -1.08447217e-01,
7.12551402e-02, -8.90705678e-02, -1.75874783e-02, -8.20507301e-02,
3.17308354e-02, -7.74069571e-02, 1.13361871e-02, -9.66108169e-02,
7.85999597e-02, 2.15834486e-01, -4.32908540e-02, 1.34863565e-01,
-3.80695799e-03, 8.09941285e-02, -1.33292124e-02, -5.84623451e-02,
7.51708486e-02, 1.15424306e-01, -7.27280790e-02, 2.22252113e-02,
1.56402999e-01, 9.00184662e-02, 6.22957358e-03, 4.45413700e-03,
-1.79916285e-02, -8.23709168e-02, -9.94830658e-03, -1.99626403e-02,
9.47451880e-02, 4.21276074e-02, -9.24379383e-02, 1.39201859e-01,
-1.94021455e-01, 1.07499636e-01, -2.17960619e-02, 1.24959083e-01,
-5.36106346e-02, -2.05054406e-01, -3.86857696e-02, 6.26904597e-02,
-1.06876941e-01, 3.75400447e-02, -5.62579252e-02, -2.41012882e-02,
-5.78505174e-02, 9.70506314e-02, 4.88624698e-02, 9.01966546e-03,
4.26860904e-02, -9.76559453e-02, -7.60155268e-02, -9.32302871e-02,
-2.07964942e-01, 8.47002030e-02, 1.48508689e-02, -3.16250331e-02,
-6.52772611e-02, -4.10257852e-02, -6.72812808e-02, 3.39399239e-02,
-2.46794507e-02, 2.82255488e-02, -9.83309293e-03, -1.12212639e-01,
3.68046323e-02, 1.58435551e-01, -1.60384599e-01, -1.11470595e-01,
5.65803748e-02, 7.27597725e-02, 1.26971237e-01, -5.69599447e-03,
-1.04505195e-01, 1.30238298e-02, -4.81125357e-02, -1.29461499e-01,
-6.59886060e-02, 4.64535279e-02, -1.62860824e-02, 4.89595040e-02,
7.52418661e-02, 2.02746308e-01, -9.42111714e-02, 1.02668115e-01,
-1.03124594e-01, -6.43021780e-02, 2.71891204e-02, -9.65181795e-02,
1.52550445e-01, -4.25016904e-02, -8.03019570e-02, 9.95801064e-02,
8.24005271e-02, 9.61957157e-02, -1.47736752e-01, -4.57647941e-02,
-6.55683561e-03, 2.56885379e-01, 4.95095955e-02, -3.84886390e-02,
-1.63762448e-01, -1.86326278e-01, -3.96563499e-02, -2.60891662e-01,
5.98106967e-02, 5.95193869e-02, -2.94034017e-02, -9.97794933e-03,
1.16089004e-01, -5.66198735e-02, -7.83677969e-02, 5.12094010e-02,
-2.85580609e-02, 2.10780937e-02, 4.59368329e-02, 7.55939616e-02,
9.03651849e-02, 7.37273405e-02, -2.48958219e-02, 7.15584530e-02,
5.31523076e-02, -1.30704265e-02, 2.45607645e-02, 1.03559631e-01,
-1.24757044e-01, 2.29375300e-02, 1.77481790e-02, -1.44692850e-01,
1.83641936e-02, -5.72485545e-03, -5.97195784e-02, 5.96419496e-02,
8.57298250e-02, 8.13006377e-03, -1.89875793e-01, 9.97943681e-02,
8.46199867e-02, 1.50010743e-01, -5.45163845e-02, -2.89238351e-02,
-4.86058705e-03, -1.55315804e-01, -1.52953444e-01, 2.01107118e-01,
-6.94985846e-02, -9.98206292e-02, -1.08779961e-01, -6.50690144e-02,
3.04791857e-02, -9.29300930e-03, -5.15198805e-02, -1.67610775e-01,
2.71715403e-02, -6.36411651e-02, 1.56951026e-01, -7.38105541e-02,
3.79029639e-02, 5.61590830e-02, -2.71916144e-02, 7.01228450e-02,
-4.21951403e-02, 2.22401159e-02, 1.61788597e-02, 1.47784436e-02,
1.13670900e-02, 2.32787318e-03, -3.01547378e-02, 9.86237679e-02,
8.43347378e-02, 2.52329473e-02, 1.94827514e-02, -9.32721054e-02,
-5.17718576e-02, 6.69520777e-02, 8.85230328e-02, 1.28158888e-01,
-3.20705375e-02, 9.83802811e-03, -8.04382898e-02, -2.59990161e-02,
-1.07081847e-01, -7.61793678e-02, -1.21202096e-01, -3.71143607e-02,
1.65045440e-01, -8.07852953e-02, -4.26651591e-02, -1.60423800e-01,
-4.85852247e-02, 1.26566022e-01, -8.89879828e-02, -2.04655478e-01,
-1.90122047e-01, -1.02882075e-01, 6.97891803e-02, 1.56354022e-02,
1.31113975e-01, -7.26021503e-02, 6.61399960e-02, 1.87082337e-01,
9.01168289e-02, 1.15031695e-01, -7.83808741e-02, -1.33216615e-01,
1.02587647e-02, -1.89608379e-02, 2.50649977e-02, 1.30910580e-01,
-1.31668220e-01, -4.08945116e-02, 4.22584845e-03, -2.13350698e-01,
3.03030546e-02, 2.99598655e-02, 4.81247112e-02, -7.67847263e-02,
3.84417186e-02, 8.61802475e-02, -1.99951989e-01, 2.40980408e-02,
-1.29018358e-01, 3.65316072e-02, -4.53713505e-02, -7.10502550e-02,
-5.20098356e-02, 3.04094308e-02, 7.52992839e-02, 6.61186909e-02,
-9.67867938e-02, -1.29195917e-04, -5.19479750e-02, 1.48578528e-01,
3.23400273e-02, -2.17161703e-02, -1.04817781e-01, 7.44292736e-02,
-5.41295739e-02, -6.79119876e-02, -2.32050643e-01, -4.98423585e-02,
-2.16949754e-01, 5.96252846e-02, 4.32523792e-02, 4.56964495e-02,
-1.17961168e-01, -1.43334157e-01, 7.34100096e-04, 7.56813323e-02,
9.12146646e-02, 1.83877144e-02, -2.00347068e-01, 7.17208061e-02,
1.09144395e-01, -5.21044513e-02, 3.76149041e-02, 3.86468665e-02,
1.00399705e-01, -4.61556204e-03, 3.39164434e-02, 5.65848462e-02,
-6.50537821e-03, 1.32600846e-02, -1.16110013e-01, 3.69347877e-03,
9.11290728e-02, 1.55042989e-02, -1.69306132e-01, -5.42772881e-02,
-1.70641253e-01, -9.37610651e-02, -5.88636311e-02, 4.05188810e-02,
-3.62855884e-02, 1.01757716e-01, 8.63622845e-02, 5.76912980e-02,
7.13985155e-02, -8.84397562e-02, 1.51479199e-01, -8.15588867e-02,
5.43494704e-02, 2.10977263e-01, -1.26613525e-01, -1.14998324e-01,
2.30437719e-02, 2.61509881e-03, -2.27291280e-02, -9.04926242e-02,
-3.78487241e-02, 2.67542602e-02, 3.64966414e-02, -1.28593177e-01,
-2.82797756e-02, -1.25953855e-01, 8.03372263e-02, -5.15399243e-02,
1.42018759e-02, -6.53924392e-02, -8.90653460e-03, 1.12026821e-01,
-9.53956457e-02, 1.22187934e-02, 6.16323352e-02, 9.16076238e-02,
1.14829890e-01, -1.83868074e-01, -7.48231957e-02, 1.91085627e-01,
1.85541822e-02, -1.06773543e-01, -9.54505328e-02, 8.10870389e-02,
-8.90828545e-02, -6.87272064e-02, -1.59339146e-02, -2.72853863e-02,
-1.70806059e-01, 2.96515319e-02, 5.91177207e-02, 3.00651099e-02,
-4.82497318e-02, -1.68193674e-01, 6.57138823e-02, 3.98445330e-02,
-8.76130768e-02, 1.76332512e-01, 1.36117990e-01, -1.28518233e-03,
-6.14667434e-02, 1.10217459e-01, 5.96002935e-02, 1.29378868e-01,
-1.37550331e-01, 3.73099805e-02, 9.76899824e-03, -7.12450165e-02,
-1.41369429e-01, 1.65226077e-01, -4.46207280e-02, -6.84757925e-02,
8.04109419e-02, -4.65845484e-02, 1.28429729e-01, -8.35858270e-02,
1.83522192e-02, 9.03509014e-03, 1.70358769e-01, 1.36397516e-01,
-2.83933902e-02, 8.44143664e-02, -5.68204796e-02, -2.24114456e-02,
-6.58831169e-02, -4.57375862e-02, -2.62972119e-02, 1.31088121e-01,
-1.09551095e-01, -4.92194966e-02, 7.05350504e-02, -1.06664752e-01,
6.22597671e-02, 8.40205575e-02, 1.58067926e-01, -4.92237043e-02,
-3.81962554e-02, 4.13209964e-02, 4.92026288e-02, -9.54111935e-02,
1.86121073e-01, 9.23164162e-03, 8.40616050e-02, 8.30168882e-02,
1.02190104e-01, -4.40549939e-02, 3.54043816e-02, 4.88904642e-02,
1.15819869e-01, 1.10332748e-01, -3.26431420e-01, 1.45556268e-01,
5.39322790e-02, -2.34555612e-02, -4.18357562e-02, -3.91941445e-02,
6.16007404e-02, 5.65514374e-03, 1.65918797e-01, -8.71656039e-02,
1.09761792e-01, 1.39151800e-01, -2.25599785e-04, 1.56203245e-02,
9.89700603e-02, 2.10704695e-02, 1.07903297e-01, 3.96906472e-02,
7.24655119e-02, -1.39428925e-02, -1.44823484e-02, -6.37526454e-02,
-1.51457881e-01, 1.65227574e-01, 8.20730098e-02, -2.90206465e-02,
6.92388122e-02, -6.95454368e-02, -2.15717327e-02, -1.91239708e-01,
3.80513543e-02, -1.00919586e-01, -2.42957797e-02, 2.25686982e-02,
-5.15553000e-02, 1.11441279e-02, 1.44969048e-01, 5.87027186e-02,
-1.35397452e-01, -9.99100943e-02, -9.45110401e-02, -1.10175312e-02,
-9.08042564e-02, -8.42855236e-02, -3.93150500e-02, -6.27285431e-02,
5.07541421e-02, -1.10767977e-02, -5.35497174e-02, -1.14192939e-01,
-1.36079386e-01, -7.38767910e-03, 1.09356388e-01, 1.91517901e-02,
3.05371604e-02, -2.68382037e-02, 9.25096061e-02, 4.14303435e-02,
-6.57719466e-02, 7.10789053e-02, -5.00398784e-02, -6.18737343e-02,
1.36755045e-03, -5.49308558e-02, 6.38548168e-03, 1.50716804e-02,
-1.04259839e-01, -5.26867268e-04, 1.74846560e-02, -8.72175256e-02,
7.12830078e-02, -1.10566839e-01, -6.99686111e-03, -2.03523093e-01,
3.08655052e-02, -4.03217311e-02, 8.03534621e-02, -4.25909323e-03,
1.78006309e-02, 5.78925175e-02, 6.05481563e-02, 1.15122819e-01,
-8.79641884e-02, -7.28182565e-02, 1.15268203e-01, -1.25190091e-01,
1.69868187e-01, 2.78768236e-02, -5.49236431e-02, 8.79345272e-02,
1.55172759e-01, -3.35516470e-02, 1.94933650e-02, 1.09683279e-01,
7.38649040e-02, 2.71889487e-02, -1.02203236e-01, 6.26739718e-02,
3.01212939e-02, 8.55295435e-02, -8.99555152e-02, 5.75196520e-02,
9.65068843e-02, -2.34338695e-02, 5.11524000e-02, 9.59786979e-02,
-4.09009270e-03, -4.34284654e-03, 7.75102962e-02, -9.71237550e-02,
2.49424335e-02, -2.42976067e-02, 1.17062379e-01, 1.24592745e-01,
1.11873209e-02, 2.86462300e-02, -9.86969290e-02, -7.07860827e-02,
3.26677339e-01, -9.32341096e-02, 4.44032822e-03, 2.03391567e-01,
1.25322922e-01, -6.13731658e-02, 2.67250403e-02, -1.02302802e-01,
-5.46276533e-02, -9.24825590e-02, 1.74442055e-01, -2.36831098e-02,
1.04452982e-01, 1.68302812e-01, 1.28141798e-01, -1.38941701e-01,
-9.08718773e-02, 3.38724564e-02, 3.93973870e-01, -1.35517549e-02,
-2.27050321e-01, -4.24147992e-02, 2.70738761e-01, -2.31271024e-01,
4.17720047e-02, -1.10417595e-01, 4.32469351e-02, -3.79741991e-02,
1.11490712e-02, -2.35608123e-01, 5.59919881e-03, -1.84273591e-02,
4.30270210e-03, 1.07343877e-01, 8.73628859e-02, 3.92284505e-02,
2.08237312e-01, -1.50396207e-01, -5.78071600e-02, 1.09050064e-01,
-1.72560508e-01, -5.29250048e-03, -4.30020691e-05, -1.09535915e-01,
-6.88224221e-02, -1.16652351e-01, -6.08346479e-02, -1.10479863e-01,
2.39838393e-02, -1.29158555e-01, -1.33933131e-02, 9.75715374e-02,
5.20726807e-02, 1.00214419e-02, 1.24303848e-01, -3.79805143e-02,
-2.02666428e-01, 8.38718202e-02, -9.11335698e-02, 7.95591754e-02,
-5.81698323e-02, -5.34511292e-02, -6.17459653e-02, 2.60544183e-02,
3.90948395e-03, 1.19604571e-01, -7.07347635e-02, -1.12078120e-01,
-4.96179879e-02, 1.11526713e-02, -7.07221651e-02, 7.69144196e-02,
1.58613041e-01, -1.39781026e-01, 2.95793752e-02, 3.68394110e-02,
-4.18078127e-02, -1.60757015e-01, 1.47893762e-01, -9.84282057e-03,
1.89614416e-01, -2.38628477e-02, -1.32418300e-01, -1.68296482e-01,
1.25698533e-01, 1.05774445e-01, -3.71804423e-02, -2.13593768e-01,
3.19594448e-02, 1.54781061e-03, 2.20367778e-03, 2.07988598e-02,
5.41224126e-02, -9.23232942e-02, 1.70750438e-01, -5.27122468e-02,
9.25312776e-04, 9.01657075e-02, -2.20170682e-02, -2.11158265e-03,
-7.54551525e-02, 9.53720140e-03, 7.55578265e-02, -1.23155254e-02,
1.04368406e-01, 4.28191715e-02, 1.23672910e-01, -2.77525048e-02,
1.11384424e-01, 6.39740767e-02, -1.88260677e-02, -1.15043418e-01,
3.22372753e-02, -1.01225379e-02, -1.37108132e-01, 6.97854432e-02,
1.17521249e-01, -2.51552568e-02, -1.77961417e-01, 5.31862795e-02,
-1.41220603e-01, 2.14986461e-01, -1.08034184e-01, -1.84180491e-02,
7.79878087e-03, -9.05938863e-02, -4.83248139e-02, -9.60869016e-02,
-6.97913023e-02, -1.16907469e-02, 6.10202025e-02, -5.78486811e-02,
2.06700089e-01, 1.24277208e-01, 1.91080816e-01, -6.47910259e-03,
1.75225356e-01, -8.44110722e-02, 5.01478987e-02, -8.56551337e-02,
5.17711965e-02, 6.42261643e-02, 2.22894036e-01, -6.07027633e-02,
2.05478927e-02, 1.37951283e-01, -2.13021341e-02, 3.09921472e-02,
5.50481297e-02, 7.65550546e-02, 9.54117672e-02, 9.90553973e-02,
1.28249736e-01, -1.28388305e-01, 1.99409425e-02, 5.41317405e-02,
1.65428199e-02, -7.79161700e-03, -2.22760338e-01, 1.44991728e-01,
-5.24649010e-02, -5.92774404e-02, -1.03581415e-02, 1.04159726e-01,
1.29533429e-01, 1.70063520e-02, 1.04111676e-02, -2.23362998e-02,
-3.62960885e-02, -4.59477709e-02, 4.30522613e-02, 1.19699534e-01,
5.77504464e-02, 1.84266394e-01, 3.75006804e-03, 9.89718511e-02,
4.59842839e-02, -5.83119485e-02, -8.86614216e-02, -4.26700382e-02,
1.58807757e-01, 1.51974708e-02, -1.26840250e-03, -1.22019981e-02,
3.08935079e-01, 4.63270561e-02, -1.63488044e-03, -1.49984190e-01,
9.75082102e-02, -6.29723805e-02, -1.13820938e-01, -7.31180915e-03,
-1.10964502e-01, 5.49700398e-02, 9.07988325e-02, -6.90418252e-02,
1.29555693e-02, 7.62790039e-02, 1.00664394e-01, 2.57607467e-02,
-1.14079824e-02, 1.53364129e-01, -1.24106507e-01, -1.70289728e-01,
3.07791554e-02, -8.96111751e-02, -2.97177200e-02, -6.71701998e-02,
9.10907016e-03, 1.09873706e-01, -9.82484282e-02, 5.50252596e-03,
1.06404189e-01, -9.65272669e-02, -3.92007789e-02, -1.00951851e-01,
-1.02342179e-01, -6.50844336e-03, 4.57039361e-02, 2.60436807e-02,
-1.99107088e-01, 6.80906526e-02, 2.02862457e-02, 1.98220654e-01,
-1.24779797e-01, -1.11222435e-01, 1.24684603e-03, 8.84841212e-02,
-6.65867690e-02, -1.37476842e-01, -1.64705015e-01, -3.39106357e-02,
4.88768752e-02, 8.48970262e-03, 1.86168310e-02, -1.92014889e-02,
-4.00592266e-02, 6.79770519e-02, -8.09714789e-02, 3.83053876e-02,
1.15890411e-01, 4.57180162e-02, -1.78226887e-01, 7.16453531e-02,
-9.42551537e-02, 5.79174643e-02, -1.82654212e-02, -1.11120696e-01,
-1.30939303e-02, 3.69285182e-02, 1.04544790e-01, -2.87094715e-03,
-7.45169678e-02, -2.64419296e-02, -1.77889916e-01, -1.15789079e-01,
2.35601282e-01, -5.94735448e-02, -8.98569813e-02, 8.75017377e-02,
3.05196247e-02, -9.09946181e-03, 5.32243018e-02, 1.01669495e-01,
6.80861028e-03, -1.39142521e-01, -9.64457416e-02, 7.18267539e-02,
-7.59109154e-02, 1.45036711e-01, 1.17190105e-01, 1.80500781e-01,
-1.28377262e-02, 3.05742413e-02, -4.59354531e-02, -8.60945625e-02,
2.47108553e-01, -4.41058798e-02, 8.97614722e-03, -1.16175549e-01,
-3.11678657e-02, -3.15132743e-02, -1.70303007e-03, 1.02449023e-01,
1.44831377e-01, -4.23111810e-02, -1.04496701e-01, -5.02864641e-02,
-1.77470952e-01, 5.70196206e-03, -1.21004897e-01, 1.02390113e-01,
-4.51532500e-02, 2.15086429e-02, -4.01693302e-02, 1.23775032e-01,
-1.00373951e-02, 1.05200593e-01, -2.92123459e-01, 1.58435840e-01,
4.02348404e-02, -1.95641132e-02, -2.11935134e-03, 1.81223475e-01,
-5.14744417e-02, -7.16209038e-02, -9.45797123e-02, 1.19286097e-02,
-1.00280922e-01, -1.00878816e-01, 3.87653314e-02, -2.41592201e-02,
-1.84317158e-03, 3.18474547e-02, -2.04477917e-01, 2.91607947e-02,
1.00567001e-01, 6.04537064e-02, -7.73523227e-03, 6.30822799e-02,
-2.96948132e-02, 2.28529429e-01, 5.82197923e-02, -1.74129026e-01,
-2.41114605e-01, 2.43244244e-02, 3.01107604e-02, 1.82384292e-01,
1.15662815e-01, -3.97686032e-02, -5.80240689e-03, 4.23530125e-02,
8.47157181e-02, 4.41112710e-02, -1.03665217e-02, 1.66006498e-01,
1.09792013e-01, 4.54716458e-02, 4.54465296e-02, -8.30272813e-02,
4.73785624e-02, -6.77515329e-02, 7.16185061e-02, 1.16991266e-01,
3.07325732e-02, -5.78692573e-02, -6.28055348e-02, 7.80415184e-02,
-4.39636574e-02, -1.71740127e-02, -1.04629639e-01, -1.08860793e-02,
1.50631938e-01, -7.60693647e-02, -5.91960387e-02, 8.64891111e-03,
1.00587787e-01, 1.22685791e-01, 1.45965570e-01, 1.58254921e-02,
2.66944159e-02, 1.85449163e-02, 6.49610177e-02, 1.50889209e-01,
-1.03866292e-01, 1.52104795e-01, -2.10776265e-02, -1.07919457e-01,
-1.15194517e-02, -2.72770323e-02, 4.69492985e-02, -9.25582542e-02,
-7.19306490e-02, -9.24352647e-02, 3.00890814e-02, 6.07024756e-02,
8.40467977e-02, 9.58729231e-02, 2.22074911e-01, 1.37396848e-02,
-1.12782908e-01, -1.32617179e-02, 5.12865057e-02, 3.05592951e-02,
7.38673064e-02, 8.58417577e-02, 3.22918249e-02, -8.28546841e-02,
2.07313049e-01, -9.23590512e-02, -1.26355087e-01, -3.44102443e-02])
我们可以验证一下通过正态分布随机产生的数据集合的平均值是否为最开始我们设定的
mu
的值:
# 误差小于0.01时,说明两个数相等
print("mu==平均值:", abs(mu - np.mean(s)) < 0.01)
mu==平均值: True
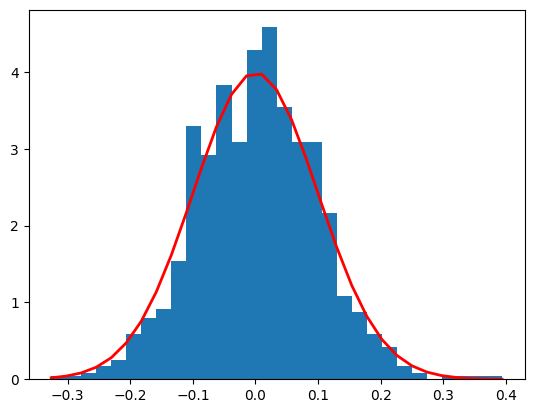
最后让我们对上面生成的数据集合进行统计,得到正态分布的分布图像:
89.10. 方差和标准差#
方差,用以表示数据集中数据点的离散程度,其数学定义为:
其中 \(\overline{x}\) 表示 \(x\) 的平均值,即 \(\overline{x}=\frac{x_1+x_2+...+x_n}{n}\)。
标准差也表示数据集中数据点的离散程度,它在数学定义上其实就是方差的平方根:
我们可以使用
np.std(x,
ddof=1))
来计算任意数据集合
\(x\)
的标准差。
接下来,我们就利用该函数计算一下上面服从正态分布的随机变量的标准差,并且判断该标准差是否和初始化传入的
sigma
参数相等:
std = np.std(s, ddof=1)
# 误差小于 0.01 则认为相等
print("sigma==标准差:", abs(sigma - std < 0.01))
sigma==标准差: True
综上,我们可以知道当数据 \(x\sim N(\mu,\sigma^2)\)时, \(\mu\) 为数据集合 \(x\) 的均值,\(\sigma\) 为数据集合 \(x\) 的标准差。
89.11. 数学期望#
数学期望是试验中每次可能结果的概率乘以其结果的和。它反应了随机变量的平均取值大小。
离散型随机变量的数学期望如下:
其中 \(p_k\) 为离散型变量的概率质量函数。
连续型随机变量的数学期望如下:
其中 \(f(x)\) 为连续型变量的概率密度函数。
89.12. 协方差#
在概率论和统计学中,协方差被用于衡量两个变量之间的总体误差。方差是协方差的一种特殊情况,即当两个变量相同时,这两个变量的协方差就等于方差。
假设需要衡量的变量分别为 x ,y 。则它们的协方差的公式定义如下:
其中 \(\overline{x}\) 和 \(\overline{y}\) 表示变量的平均值。
当 \(x=y\) 时,上面的式子就可以化为方差的计算公式,如下:
若协方差为正则表示两个变量呈正相关,若协方差为负则表示两个变量呈负相关。
我们可以使用
numpy.cov()
函数对协方差进行计算。
注意:numpy.cov(X)
得到的是一个协方差矩阵,又叫相关矩阵。也就是说,该函数可以计算多组变量之间的协方差值。传入参数
\(X\)
是一个矩阵。该矩阵的每一列都是一组独立的数据集。如下:
x = [1, 2, 3]
y = [3, 1, 1]
a = np.array([x, y])
# 传入的参数 a 的每一列都是一组数据集
A = np.cov(a)
A
array([[ 1. , -1. ],
[-1. , 1.33333333]])
从上面的结果可以看出,我们利用
numpy.cov()
得到了一个协方差矩阵 A,且该矩阵大小为
\(2\times 2\)。
-
\(A_{11}\) 表示第一列和第一列的协方差,即数据集 \(x\) 与 数据集 \(x\) 的协方差,即数据集 \(x\) 的方差。
-
\(A_{22}\) 表示第二列和第二列的协方差,即数据集 \(y\) 与 数据集 \(y\) 的协方差,即数据集 \(y\) 的方差。
-
\(A_{12}\) 表示第一列和第二列的协方差,即数据集 \(x\) 与 数据集 \(y\) 的协方差。
-
\(A_{21}\) 表示第二列和第一列的协方差。其实和 \(A_{12}\) 的性质是一样的,\(A_{21}\)=\(A_{12}\)。
同理,当传入的是一个
\(n \times 3\)
的矩阵(其中 3 代表列数,即数据集的个数。\(n\)
代表行数,即每个数据集中的样本数)时,np.cov()
得到的就是一个
\(3\times 3\)
的协方差矩阵。当传入的是一个
\(n\times m\)
的矩阵时,
np.cov()
得到的就是一个
\(m \times m\)
的协方差矩阵
\(A\)。其中
\(A_{i,j}\)
的值就是第
\(i\)
列数据与第
\(j\)
列数据的协方差。
89.13. 统计学相关概念#
89.14. 样本和总体#
-
总体:在进行统计分析时,研究对象的全部。可以用 \(X\) 表示。
-
样本:从总体 \(X\) 中按照一定的规则抽出的个体,用 \(X_1,X_2,...X_n\)表示。
-
样本容量:样本中所含个体的个数被称之为样本容量,用 \(n\) 表示。
举个例子,假设我们需要调查全国青少年的平均身高。身高这个研究变量就是研究对象。全国青少年的身高就为总体 \(X\)。但是我们不可能对所有青少年的身高进行调查,一般只能通过抽样得到部分数据,然后利用部分数据对总体的身高值进行估计。
其实这里通过抽样得到的部分数据就叫做样本。
从整体抽出一个个体,就是对总体 \(X\) 进行一次抽样并记录结果。在相同条件下对总体进行 \(n\) 次独立抽样。将 \(n\) 次抽样结果按照试验顺序记为 \(X_1,X_2,...,X_n\)。他们是相互独立的,且都是与 \(X\) 具有相同分布的随机变量。\(X_1,X_2,...,X_n\) 称之为来自总体 \(X\) 的一个简单随机样本。
89.15. 假设检验的概念#
假设检验是统计学中非常重要的概念。它的逻辑类似于反证法。设立一个原假设和一个与之对立的备选假设。
在原假设的前提下,进行实验,如果发生了不可能事件或者几率很小的事件 ,那么我们就可以认为原假设不合理,应当被拒绝。而与之对应的备选假设合理,应该被接受。
举个例子,有一种奶茶是由牛奶和茶按照一定比例混合而成。在制作该奶茶时,我们可以先加奶后加茶(记为 MT),也可以先加茶后加奶(记作 TM)。我有个同学叫小红,她声称她自己具有辨别 MT 和 TM 的能力。那么如何判别她是否真的具有这种能力呢?我们就可以使用假设检验。假设原假设 \(H_0\) 为:
如果上面这个假设是正确的,那么小红对任意一杯奶茶鉴别准确的概率为:0.5(也就是随机鉴别)。
现在我准备了 10 杯奶茶,如果原假设准确的话,那么小红全部鉴别成功的概率就为 \(p=2^{-10}=0.00097<0.001\),几乎为不可能事件。
然后实验开始,我们为小红准备了 10 杯奶茶,让她检测,最终结果是她全部检测正确了。也就是说,在原假设的条件下,发生了不可能事件。因此原假设 \(H_0\) 不合理,应当予以拒绝。而与之对应的备选假设 \(H_1\) 合理,即该同学具有这种鉴别能力。
上面的整个过程就是假设检验过程,假设检验过程的基本思想就是,小概率事件在一次实验中不会发生,如果发生了,则证明原假设应当被拒绝。
假设检验有很多种方法,大致可以根据分布函数的不同,分为 z 检验(正态分布)、t 检验(t 分布)和 F 检验(分布)。
为了方便讲解,这里我们以 z 检验为例对假设检验进行讲解。
89.16. z 检验#
z 检验是一种用于检验大样本(样本容量超过 30)的平均差异的检验方法。它用正态分布理论推断了差异发生的概率,从而比较了样本和总体平均数的差异是否显著。
z 假设检验的完整步骤如下:
-
提取总体的原假设(\(H_0\))和备选假设(\(H_1\)),并且收集样本数据。
-
假设原假设 \(H_0\) 正确,构建比较分布:正态分布。
计算样本数据在比较分布中的位置。
将结果与临界值进行对比。
-
若为小概率事件,则拒绝原假设,接受备选假设。反之则接受原假设。
小概率事件:我们认为小概率事件为 \(p<0.05\) 的事件。
比较分布:用于检验假设的分布函数,z 假设检验中使用的是正态分布。
统计量 z:正态分布的概率密度函数的面积就是该分布函数的概率值。概率值所对应的密度函数的横坐标的值就是统计量 z。
临界值:如下图所示,我们把左右两边的 2.5% 的面积定义为小概率事件,即紫色部分为小概率事件。这两个紫色区域的临界值的横坐标为: \( z = \pm 1.96\),称作统计量 z 的临界值。当通过样本计算出来的统计量 z 值小于 或者 大于临界值 ,就可以拒绝原假设。
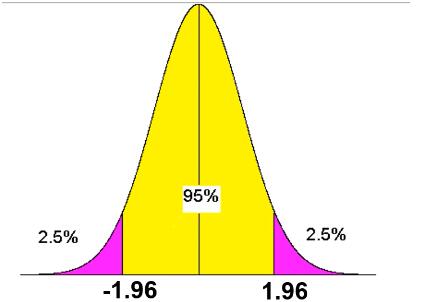
那么如何计算一个样本的统计量呢?statsmodels.stats.weightstats
库中的
ztest
可以实现这个过程。
ztest
函数包含的输入参数如下:
x1:样本的数据值。
value:原假设中总体的均值。
该函数的原假设 \(H_0\):样本 x1 所对应的均值为 value;备选假设 \(H_1\),样本 x1 所对应的均值不为 value。通过函数可以得到如下输出值:
tstats:统计量值
pvalue:p 值
如果这里存在一个样本集合 arr,让我们通过假设检验推断一下该样本对应的总体的均值是否为 \(39\)。
首先让我们来定义样本容量超过 30 的样本集合,因为只有超过 30 的样本集合的均值才能使用 z 检验进行推断。
arr = [23, 36, 42, 34, 39, 34, 35, 42, 53, 28, 49, 39, 46, 45, 39, 38, 45, 27,
43, 54, 36, 34, 48, 36, 47, 44, 48, 45, 44, 33, 24, 40, 50, 32, 39, 31]
len(arr)
36
接下来,让我们使用
ztest
计算原假设所对应的统计量 z:
import statsmodels.stats.weightstats as sw
# 原假设为总体的平均值是 39
z, p = sw.ztest(arr, value=39)
z
0.3859224924939799
从结果可以看到,原假设的统计量 z = 0.38,该值刚好大于 -1.96,小于 1.96。因此,我们应当接受原假设。
综上,我们可以得到样本所对应的总体的平均值等于 39。
如果将原假设改为:样本所对应的总体的平均值为 20。让我们重新来计算统计量 t:
z, p = sw.ztest(arr, value=20)
z
15.050977207265216
从结果可以看出,z 的值远远大于 1.96。因此,我们应当拒绝该假设,接受与之对应的备选假设,即总体的平均值不等于 20。
当然,上面的 z 检验方案只是 z 检验的一种。我们还可以按照 {临界值只有左边存在、临界值只有右边存在、临界值两边都存在} 等三种可能,将 z 检验类型分为 {左侧检验、右侧检验和双侧检验}。
利用统计量判断原假设是否拒绝并不是唯一的方法,我们还可以使用 \(p\) 值来对其进行判断。 \(p\) 值就是上面这个函数返回的第二个参数。
我们一般认为如果 \(p\) 值小于显著水平(0.05,即临界值所对应的概率),则表示拒绝原假设。若 \(p\) 值大于显著水平则接受原假设。你可以输出上面的 \(p\) 值,查看一下利用 \(p\) 值判断假设的结果和利用统计量判断的结果是否一致。
其实使用 \(p\) 值判断原假设是否应当被接受的方案比根据临界统计量判断的方案要好。因为无论我们选择任何比较分布,它的显著水平我们都可以设置为 0.05(即最小事件的概率)。但是,因为相同概率所对应的分布函数下的统计量根据分布函数不同而不同。即不同比较分布的临界统计量是不同的,而显著水平是相同的。
因此,大家都喜欢使用 \(p\) 值来判断原假设是否接受。而不是选择计算统计量,然后再找相应分布函数的临界值,然后再进行比较,最后再下结论。
其实假设检验是统计学中最重要的一部分,它还包含了很多知识点。但是由于这些知识点在机器学习中使用并不频繁(数据分析中经常使用),就不做赘述了。
89.17. 总结#
本实验首先讲解了概率论中的三大公式,这个公式在朴素贝叶斯算法中使用频繁。然后,讲解了离散分布和连续型分布的具体区别,以及常用的分布函数式子和图像。最后对统计学中的假设检验进行了相关的讲解与实现。
○ 欢迎分享本文链接到你的社交账号、博客、论坛等。更多的外链会增加搜索引擎对本站收录的权重,从而让更多人看到这些内容。