4. 多项式回归实现与应用#
4.1. 介绍#
前面的实验中，相信你已经对线性回归有了充分的了解。掌握一元和多元线性回归之后，我们就能针对一些有线性分布趋势的数据进行回归预测。但是，生活中还常常会遇到一些分布不那么「线性」的数据，例如像股市的波动、交通流量等。那么对于这类非线性分布的数据，就需要通过本次实验介绍的方法来处理。
4.2. 知识点#
多项式回归介绍
多项式回归基础
多项式回归预测
4.3. 多项式回归介绍#
在线性回归中，我们通过建立自变量 \(x\) 的一次方程来拟合数据。而非线性回归中，则需要建立因变量和自变量之间的非线性关系。从直观上讲，也就是拟合的直线变成了「曲线」。
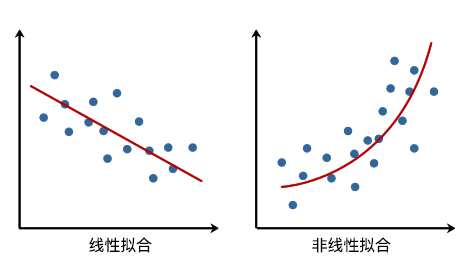
对于非线性回归问题而言，最简单也是最常见的方法就是本次实验要讲解的「多项式回归」。多项式是中学时期就会接触到的概念，这里引用 维基百科 的定义如下：
多项式（Polynomial）是代数学中的基础概念，是由称为未知数的变量和称为系数的常量通过有限次加法、加减法、乘法以及自然数幂次的乘方运算得到的代数表达式。多项式是整式的一种。未知数只有一个的多项式称为一元多项式；例如 \(x^2-3x+4\) 就是一个一元多项式。未知数不止一个的多项式称为多元多项式，例如 \(x^3-2xyz^2+2yz+1\) 就是一个三元多项式。
4.4. 多项式回归基础#
首先，我们通过一组示例数据来认识多项式回归
# 加载示例数据
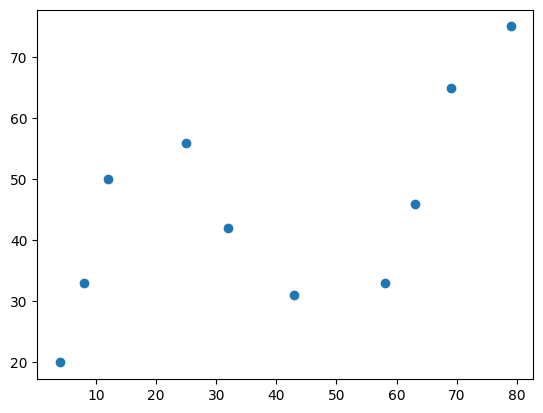
x = [4, 8, 12, 25, 32, 43, 58, 63, 69, 79]
y = [20, 33, 50, 56, 42, 31, 33, 46, 65, 75]
示例数据一共有 10 组，分别对应着横坐标和纵坐标。接下来，通过 Matplotlib 绘制数据，查看其变化趋势。
from matplotlib import pyplot as plt
%matplotlib inline
plt.scatter(x, y)
<matplotlib.collections.PathCollection at 0x11ba8aa70>
4.5. 实现 2 次多项式拟合#
接下来，通过多项式来拟合上面的散点数据。首先，一个标准的一元高阶多项式函数如下所示：
其中，\(m\) 表示多项式的阶数，\(x^j\) 表示 \(x\) 的 \(j\) 次幂，\(w\) 则代表该多项式的系数。
当我们使用上面的多项式去拟合散点时，需要确定两个要素，分别是：多项式系数 \(w\) 以及多项式阶数 \(m\)，这也是多项式的两个基本要素。
如果通过手动指定多项式阶数 \(m\) 的大小，那么就只需要确定多项式系数 \(w\) 的值是多少。例如，这里首先指定 \(m=2\)，多项式就变成了：
当我们确定 \(w\) 的值的大小时，就回到了前面线性回归中学习到的内容。
首先，我们构造两个函数，分别是用于拟合的多项式函数，以及误差函数。
def func(p, x):
# 根据公式，定义 2 次多项式函数
w0, w1, w2 = p
f = w0 + w1 * x + w2 * x * x
return f
def err_func(p, x, y):
# 残差函数（观测值与拟合值之间的差距）
ret = func(p, x) - y
return ret
接下来，就是使用最小二乘法求解最优参数的过程。这里为了方便，我们直接使用 Scipy 提供的最小二乘法类，得到最佳拟合参数。当然，你完全可以按照线性回归实验中最小二乘法公式自行求解参数。不过，实际工作中为了快速实现，往往会使用像 Scipy 这样现成的函数，这里也是为了给大家多介绍一种方法。
import numpy as np
from scipy.optimize import leastsq
p_init = np.random.randn(3) # 生成 3 个随机数
# 使用 Scipy 提供的最小二乘法函数得到最佳拟合参数
parameters = leastsq(err_func, p_init, args=(np.array(x), np.array(y)))
print("Fitting Parameters: ", parameters[0])
Fitting Parameters: [ 3.76893130e+01 -2.60474246e-01 8.00078197e-03]
Note
关于
scipy.optimize.leastsq()
的具体使用介绍，可以阅读
官方文档。特别注意的是，上面我们定义的
p_init
并不是官方文档中最小化初始参数的意思，因为最小二乘法是解析解，其不会涉及到从某个参数开始迭代的过程。实际上，这里
p_init
的具体取值不会影响求解结果，所以我们使用了随机值，但是其值的个数决定了最终多项式的次数。具体来说，\(n\)
个值则最终求解出的是
\(n-1\)
次多项式。
我们这里得到的最佳拟合参数
\(w_0\),
\(w_1\),
\(w_2\)
依次为
3.76893117e+01,
-2.60474147e-01
和
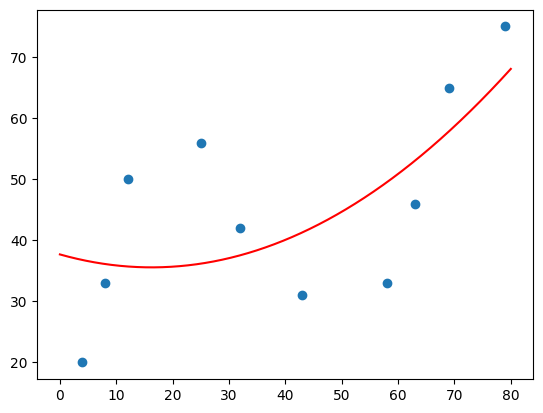
8.00078082e-03。也就是说，我们拟合后的函数（保留两位有效数字）为：
然后，我们尝试绘制出拟合后的图像。
# 绘制拟合图像时需要的临时点
x_temp = np.linspace(0, 80, 10000)
# 绘制拟合函数曲线
plt.plot(x_temp, func(parameters[0], x_temp), "r")
# 绘制原数据点
plt.scatter(x, y)
<matplotlib.collections.PathCollection at 0x10410ee00>
4.6. 实现 N 次多项式拟合#
你会发现，上面采用 2 次多项式拟合的结果也不能恰当地反映散点的变化趋势。此时，我们可以尝试 3 次及更高次多项式拟合。接下来的代码中，我们将针对上面 2 次多项式拟合的代码稍作修改，实现一个 N 次多项式拟合的方法。
def fit_func(p, x):
"""根据公式，定义 n 次多项式函数"""
f = np.poly1d(p)
return f(x)
def err_func(p, x, y):
"""残差函数（观测值与拟合值之间的差距）"""
ret = fit_func(p, x) - y
return ret
def n_poly(n):
"""n 次多项式拟合"""
p_init = np.random.randn(n) # 生成 n 个随机数
parameters = leastsq(err_func, p_init, args=(np.array(x), np.array(y)))
return parameters[0]
可以使用 \(n=3\)（2 次多项式） 验证一下上面的代码是否可用。
n_poly(3)
array([ 8.00077925e-03, -2.60474017e-01, 3.76893101e+01])
此时得到的参数结果和公式
\((3)\)
的结果一致，只是顺序有出入。这是因为 NumPy 中的多项式函数
np.poly1d(3)
默认的样式是：
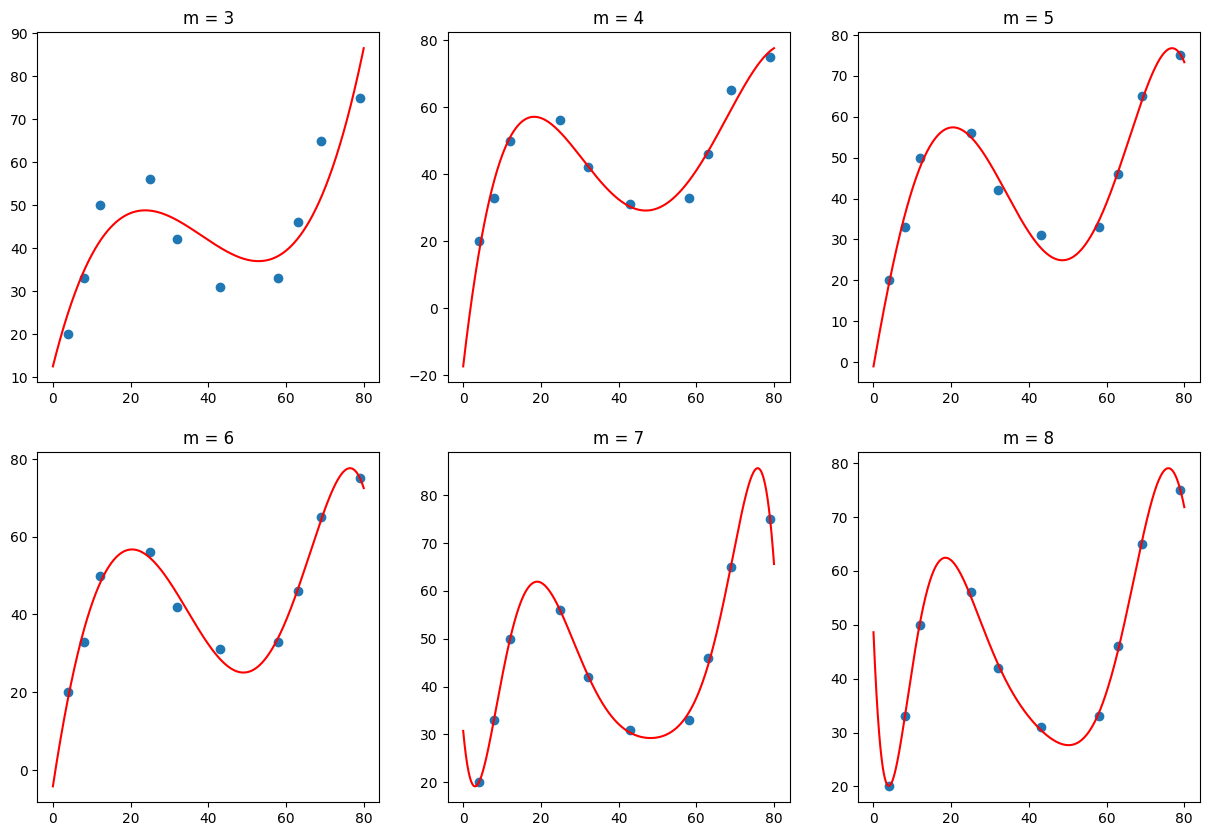
接下来，我们绘制出 3，4，5，6，7, 8 次多项式的拟合结果。
# 绘制拟合图像时需要的临时点
x_temp = np.linspace(0, 80, 10000)
# 绘制子图
fig, axes = plt.subplots(2, 3, figsize=(15, 10))
axes[0, 0].plot(x_temp, fit_func(n_poly(4), x_temp), "r")
axes[0, 0].scatter(x, y)
axes[0, 0].set_title("m = 3")
axes[0, 1].plot(x_temp, fit_func(n_poly(5), x_temp), "r")
axes[0, 1].scatter(x, y)
axes[0, 1].set_title("m = 4")
axes[0, 2].plot(x_temp, fit_func(n_poly(6), x_temp), "r")
axes[0, 2].scatter(x, y)
axes[0, 2].set_title("m = 5")
axes[1, 0].plot(x_temp, fit_func(n_poly(7), x_temp), "r")
axes[1, 0].scatter(x, y)
axes[1, 0].set_title("m = 6")
axes[1, 1].plot(x_temp, fit_func(n_poly(8), x_temp), "r")
axes[1, 1].scatter(x, y)
axes[1, 1].set_title("m = 7")
axes[1, 2].plot(x_temp, fit_func(n_poly(9), x_temp), "r")
axes[1, 2].scatter(x, y)
axes[1, 2].set_title("m = 8")
Text(0.5, 1.0, 'm = 8')
从上面的 6 张图可以看出，当 \(m=4\)（4 次多项式） 时，图像拟合的效果已经明显优于 \(m=3\) 的结果。但是随着 \(m\) 次数的增加，当 \(m=8\) 时，曲线呈现出明显的震荡，这也就是线性回归实验中所讲到的过拟和（Overfitting）现象。
4.7. 使用 scikit-learn 进行多项式拟合#
除了像上面我们自己去定义多项式及实现多项式回归拟合过程，也可以使用
scikit-learn
提供的多项式回归方法来完成。这里，我们会用到sklearn.preprocessing.PolynomialFeatures()
这个类。PolynomialFeatures()
主要的作用是产生多项式特征矩阵。如果你第一次接触这个概念，可能需要仔细理解下面的内容。
对于一个二次多项式而言，我们知道它的标准形式为：\( y(x, w) = w_0 + w_1x + w_2x^2 \)。但是，多项式回归却相当于线性回归的特殊形式。例如，我们这里令 \(x = x_1\), \(x^2 = x_2\) ，那么原方程就转换为：\( y(x, w) = w_0 + w_1x_1 + w_2x_2 \)，这也就变成了多元线性回归。这就完成了一元高次多项式到多元一次多项式之间的转换。这就类似于高中数学学习过的「换元法」。
举例说明，对于自变量向量 \(X\) 和因变量 \(y\)，如果 \(X\)：
我们可以通过 \( y = w_1 x + w_0\) 线性回归模型进行拟合。同样，如果对于一元二次多项式 \( y(x, w) = w_0 + w_1x + w_2x^2 \)，如果能得到由 \(x = x_1\), \(x^2 = x_2\) 构成的特征矩阵，即：
那么也就可以通过线性回归进行拟合了。
你可以手动计算上面的结果，但是当多项式为一元高次或者多元高次时，特征矩阵的表达和计算过程就变得比较复杂了。例如，下面是二元二次多项式的特征矩阵表达式。
还好，在 scikit-learn 中，我们可以通过
PolynomialFeatures()
类自动产生多项式特征矩阵，PolynomialFeatures()
类的默认参数及常用参数定义如下：
sklearn.preprocessing.PolynomialFeatures(degree=2, interaction_only=False, include_bias=True)
- degree: 多项式次数，默认为 2 次多项式
- interaction_only: 默认为 False，如果为 True 则产生相互影响的特征集。
- include_bias: 默认为 True，包含多项式中的截距项。
对应上面的特征向量，我们使用
PolynomialFeatures()
的主要作用是产生 2 次多项式对应的特征矩阵，如下所示：
from sklearn.preprocessing import PolynomialFeatures
X = [2, -1, 3]
X_reshape = np.array(X).reshape(len(X), 1) # 转换为列向量
# 使用 PolynomialFeatures 自动生成特征矩阵
PolynomialFeatures(degree=2, include_bias=False).fit_transform(X_reshape)
array([[ 2., 4.],
[-1., 1.],
[ 3., 9.]])
对于上方单元格中的矩阵，第 1 列为 \(X^1\)，第 2 列为 \(X^2\)。我们就可以通过多元线性方程 \( y(x, w) = w_0 + w_1x_1 + w_2x_2 \) 对数据进行拟合。
Note
本节课程中，你会看到大量的
reshape
操作，它们的目的都是为了满足某些类或函数传参的数组形状。这些操作在本实验中是必须的，因为数据原始形状（如上面的一维数组）可能无法直接传入某些特定类或函数中。但在实际工作中并不是必须的，因为你手中的原始数据集形状可能支持直接传入。所以，不必为这些
reshape
操作感到疑惑，也不要死记硬背。
前面小节中的示例数据，其自变量应该是
\(x\)，而因变量是
\(y\)。如果我们使用 2 次多项式拟合，那么首先使用
PolynomialFeatures()
得到特征矩阵。
x = np.array(x).reshape(len(x), 1) # 转换为列向量
y = np.array(y).reshape(len(y), 1)
# 使用 sklearn 得到 2 次多项式回归特征矩阵
poly_features = PolynomialFeatures(degree=2, include_bias=False)
poly_x = poly_features.fit_transform(x)
poly_x
array([[4.000e+00, 1.600e+01],
[8.000e+00, 6.400e+01],
[1.200e+01, 1.440e+02],
[2.500e+01, 6.250e+02],
[3.200e+01, 1.024e+03],
[4.300e+01, 1.849e+03],
[5.800e+01, 3.364e+03],
[6.300e+01, 3.969e+03],
[6.900e+01, 4.761e+03],
[7.900e+01, 6.241e+03]])
可以看到，输出结果正好对应一元二次多项式特征矩阵公式 \(\left [ X, X^2 \right ]\)。然后，我们使用 scikit-learn 训练线性回归模型。
from sklearn.linear_model import LinearRegression
# 定义线性回归模型
model = LinearRegression()
model.fit(poly_x, y) # 训练
# 得到模型拟合参数
model.intercept_, model.coef_
(array([37.68931083]), array([[-0.26047408, 0.00800078]]))
你会发现，这里得到的参数值和公式 \((3，4)\) 一致。为了更加直观，这里同样绘制出拟合后的图像。
# 绘制拟合图像
x_temp = np.array(x_temp).reshape(len(x_temp), 1)
poly_x_temp = poly_features.fit_transform(x_temp)
plt.plot(x_temp, model.predict(poly_x_temp), "r")
plt.scatter(x, y)
<matplotlib.collections.PathCollection at 0x1277931f0>
你会发现，上图似曾相识。它和公式 \((3)\) 下方的图其实是一致的。
4.8. 多项式回归预测#
上面的内容中，我们了解了如何使用多项式去拟合数据。那么在接下来的内容中，就使用多项式回归去解决实际的预测问题。本次预测实验中，我们使用到由世界卫生组织和联合国儿童基金会提供的「世界麻疹疫苗接种率」数据集。而目标则是预测相应年份的麻疹疫苗接种率。
首先，我们导入并预览「世界麻疹疫苗接种率」数据集。
wget -nc https://cdn.aibydoing.com/aibydoing/files/course-6-vaccine.csv
import pandas as pd
# 加载数据集
df = pd.read_csv("course-6-vaccine.csv",header=0)
df
| Year | Values | |
|---|---|---|
| 0 | 1983 | 48.676809 |
| 1 | 1984 | 50.653151 |
| 2 | 1985 | 45.603729 |
| 3 | 1986 | 45.511160 |
| 4 | 1987 | 52.882892 |
| 5 | 1988 | 62.710162 |
| 6 | 1989 | 68.354736 |
| 7 | 1990 | 73.618808 |
| 8 | 1991 | 69.748838 |
| 9 | 1992 | 69.905091 |
| 10 | 1993 | 70.517807 |
| 11 | 1994 | 62.019265 |
| 12 | 1995 | 73.887410 |
| 13 | 1996 | 73.376443 |
| 14 | 1997 | 75.599240 |
| 15 | 1998 | 71.236410 |
| 16 | 1999 | 70.783087 |
| 17 | 2000 | 72.381822 |
| 18 | 2001 | 74.997859 |
| 19 | 2002 | 72.610008 |
| 20 | 2003 | 80.104407 |
| 21 | 2004 | 75.126596 |
| 22 | 2005 | 72.750992 |
| 23 | 2006 | 85.550532 |
| 24 | 2007 | 82.033782 |
| 25 | 2008 | 76.587843 |
| 26 | 2009 | 82.602683 |
| 27 | 2010 | 80.786124 |
| 28 | 2011 | 78.931800 |
| 29 | 2012 | 83.456979 |
| 30 | 2013 | 85.124059 |
| 31 | 2014 | 87.375816 |
| 32 | 2015 | 82.704588 |
| 33 | 2016 | 85.898262 |
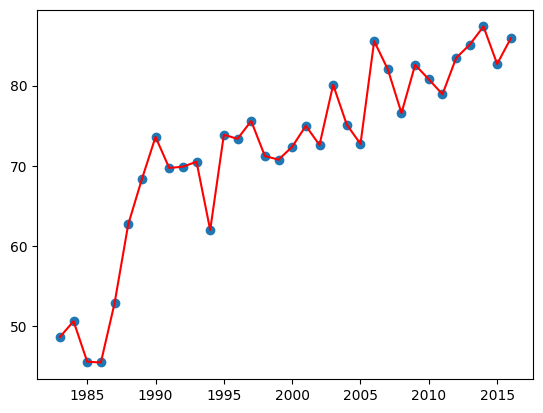
可以看出，该数据集由两列组成。其中 Year 表示年份，而 Values 则表示当年世界麻疹疫苗接种率，这里只取百分比的数值部分。我们将数据绘制成图表，查看变化趋势。
# 定义 x, y 的取值
x = df["Year"]
y = df["Values"]
# 绘图
plt.plot(x, y, "r")
plt.scatter(x, y)
<matplotlib.collections.PathCollection at 0x145e00880>
对于上图呈现出来的变化趋势，我们可能会认为多项式回归会优于线性回归。到底是不是这样呢？试一试便知。
4.9. 线性回归与 2 次多项式回归对比#
根据线性回归课程中学到的内容，在机器学习任务中，我们一般会将数据集划分为训练集和测试集。所以，这里将 70% 的数据划分为训练集，而另外 30% 则归为测试集。代码如下：
# 首先划分 dateframe 为训练集和测试集
train_df = df[: int(len(df) * 0.7)]
test_df = df[int(len(df) * 0.7) :]
# 定义训练和测试使用的自变量和因变量
X_train = train_df["Year"].values
y_train = train_df["Values"].values
X_test = test_df["Year"].values
y_test = test_df["Values"].values
接下来，我们使用 scikit-learn 提供的多项式回归预测方法来训练模型。首先，我们先解决上面的问题，那就是：多项式回归会不会优于线性回归？
首先，训练线性回归模型，并进行预测。
# 建立线性回归模型
model = LinearRegression()
model.fit(X_train.reshape(len(X_train), 1), y_train.reshape(len(y_train), 1))
results = model.predict(X_test.reshape(len(X_test), 1))
results # 线性回归模型在测试集上的预测结果
array([[81.83437635],
[83.09935437],
[84.36433239],
[85.62931041],
[86.89428843],
[88.15926645],
[89.42424447],
[90.68922249],
[91.95420051],
[93.21917853],
[94.48415655]])
有了预测结果，我们就可以将其同真实的结果进行比较。这里，我们使用到平均绝对误差和均方误差两个指标。如果你对这两个指标仍不太熟悉，它们的定义如下：
平均绝对误差（MAE）就是绝对误差的平均值，它的计算公式 \((6)\) 如下：
其中，\(y_{i}\) 表示真实值，\(\hat y_{i}\) 表示预测值，\(n\) 则表示值的个数。MAE 的值越小，说明预测模型拥有更好的精确度。
均方误差（MSE）它表示误差的平方的期望值，它的计算公式 \((7)\) 如下：
其中，\(y_{i}\) 表示真实值，\(\hat y_{i}\) 表示预测值，\(n\) 则表示值的个数。MSE 的值越小，说明预测模型拥有更好的精确度。
这里，我们直接使用 scikit-learn 提供的 MAE 和 MSE 计算方法。
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error
print("线性回归平均绝对误差: ", mean_absolute_error(y_test, results.flatten()))
print("线性回归均方误差: ", mean_squared_error(y_test, results.flatten()))
线性回归平均绝对误差: 6.011979515629812
线性回归均方误差: 43.531858295153434
接下来，开始训练 2 次多项式回归模型，并进行预测。
# 2 次多项式回归特征矩阵
poly_features_2 = PolynomialFeatures(degree=2, include_bias=False)
poly_X_train_2 = poly_features_2.fit_transform(X_train.reshape(len(X_train), 1))
poly_X_test_2 = poly_features_2.fit_transform(X_test.reshape(len(X_test), 1))
# 2 次多项式回归模型训练与预测
model = LinearRegression()
model.fit(poly_X_train_2, y_train.reshape(len(X_train), 1)) # 训练模型
results_2 = model.predict(poly_X_test_2) # 预测结果
results_2.flatten() # 打印扁平化后的预测结果
array([71.98010746, 70.78151826, 69.38584368, 67.79308372, 66.00323838,
64.01630767, 61.83229158, 59.45119011, 56.87300326, 54.09773104,
51.12537344])
print("2 次多项式回归平均绝对误差: ", mean_absolute_error(y_test, results_2.flatten()))
print("2 次多项式均方误差: ", mean_squared_error(y_test, results_2.flatten()))
2 次多项式回归平均绝对误差: 19.792070829572946
2 次多项式均方误差: 464.32903847534686
根据上面平均绝对误差和均方误差的定义，你已经知道这两个取值越小，代表模型的预测准确度越高。也就是说，线性回归模型的预测结果要优于 2 次多项式回归模型的预测结果。
4.10. 更高次多项式回归预测#
不必惊讶，这种情况是非常常见的。但这并不代表，这节实验中所讲的多项式回归就会比线性回归更差。下面，我们就试一试
3，4，5 次多项式回归的结果。为了缩减代码量，我们重构代码，并一次性得到
3 个实验的预测结果。
这里将通过实例化
make_pipeline
管道类，实现调用一次
fit
和
predict
方法即可应用于所有预测器。make_pipeline
是使用 sklearn
过程中的技巧创新，其可以将一个处理流程封装起来使用。
具体来讲，例如上面的多项式回归中，我们需要先使用
PolynomialFeatures
完成特征矩阵转换，再放入
LinearRegression
中。那么，PolynomialFeatures
+
LinearRegression
这一个处理流程，就可以通过
make_pipeline
封装起来使用。
from sklearn.pipeline import make_pipeline
X_train = X_train.reshape(len(X_train), 1)
X_test = X_test.reshape(len(X_test), 1)
y_train = y_train.reshape(len(y_train), 1)
for m in [3, 4, 5]:
model = make_pipeline(PolynomialFeatures(m, include_bias=False), LinearRegression())
model.fit(X_train, y_train)
pre_y = model.predict(X_test)
print("{} 次多项式回归平均绝对误差: ".format(m), mean_absolute_error(y_test, pre_y.flatten()))
print("{} 次多项式均方误差: ".format(m), mean_squared_error(y_test, pre_y.flatten()))
print("---")
3 次多项式回归平均绝对误差: 4.547692030677687
3 次多项式均方误差: 29.933057420285273
---
4 次多项式回归平均绝对误差: 4.424398084402177
4 次多项式均方误差: 29.02940070116114
---
5 次多项式回归平均绝对误差: 4.341616857646972
5 次多项式均方误差: 28.221932647958223
---
从上面的结果可以得出，3，4，5 次多项式回归的结果均优于线性回归模型。所以，多项式回归还是有其优越性的。
4.11. 多项式回归预测次数选择#
实验进行到现在，你可能会有一个疑问：在选择多项式进行回归预测的过程中，到底几次多项式是最优呢？
对于上面的问题，其实答案很简单。我们可以选择一个误差指标，例如这里选择 MSE，然后计算出该指标随多项式次数增加而变化的图像，结果不就一目了然了吗？试一试。
# 计算 m 次多项式回归预测结果的 MSE 评价指标并绘图
mse = [] # 用于存储各最高次多项式 MSE 值
m = 1 # 初始 m 值
m_max = 10 # 设定最高次数
while m <= m_max:
model = make_pipeline(PolynomialFeatures(m, include_bias=False), LinearRegression())
model.fit(X_train, y_train) # 训练模型
pre_y = model.predict(X_test) # 测试模型
mse.append(mean_squared_error(y_test, pre_y.flatten())) # 计算 MSE
m = m + 1
print("MSE 计算结果: ", mse)
# 绘图
plt.plot([i for i in range(1, m_max + 1)], mse, "r")
plt.scatter([i for i in range(1, m_max + 1)], mse)
# 绘制图名称等
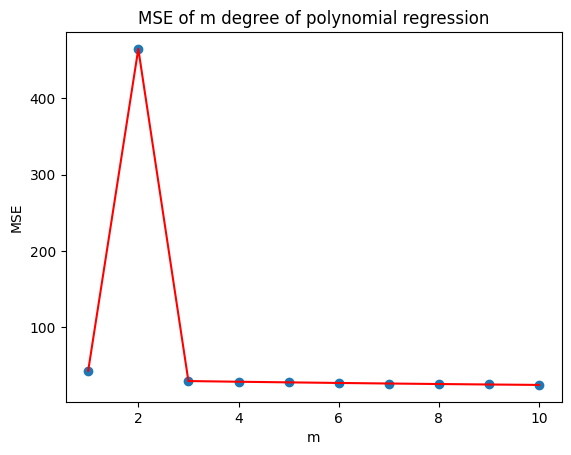
plt.title("MSE of m degree of polynomial regression")
plt.xlabel("m")
plt.ylabel("MSE")
MSE 计算结果: [43.531858295153434, 464.32903847534686, 29.933057420285273, 29.02940070116114, 28.221932647958223, 27.440821643005446, 26.712320051116773, 26.038729592942772, 25.422418053695605, 24.86581840902298]
Text(0, 0.5, 'MSE')
如上图所示，MSE 值在 2 次多项式回归预测时达到最高点，之后迅速下降。而 3 次之后的结果虽然依旧呈现逐步下降的趋势，但趋于平稳。一般情况下，我们考虑到模型的泛化能力，避免出现过拟合，这里就可以选择 3 次多项式为最优回归预测模型。
4.12. 总结#
本次实验中，我们了解了什么是多项式回归，以及多项式回归与线性回归之间的联系与区别。同时，实验探索了动手实现多项式回归拟合，以及运用 scikit-learn 在真实数据集下构建多项式回归预测模型。
相关链接
○ 欢迎分享本文链接到你的社交账号、博客、论坛等。更多的外链会增加搜索引擎对本站收录的权重，从而让更多人看到这些内容。